算法：记忆化搜索知识

1. 记忆化搜索简介

记忆化搜索（Memoization Search）：是一种通过存储已经遍历过的状态信息，从而避免对同一状态重复遍历的搜索算法。

记忆化搜索是动态规划的一种实现方式。在记忆化搜索中，当算法需要计算某个子问题的结果时，它首先检查是否已经计算过该问题。如果已经计算过，则直接返回已经存储的结果；否则，计算该问题，并将结果存储下来以备将来使用。

举个例子，比如「斐波那契数列」的定义是：f(0)=0,f(1)=1,f(n)=f(n−1)+f(n−2)。如果我们使用递归算法求解第 n 个斐波那契数，则对应的递推过程如下：

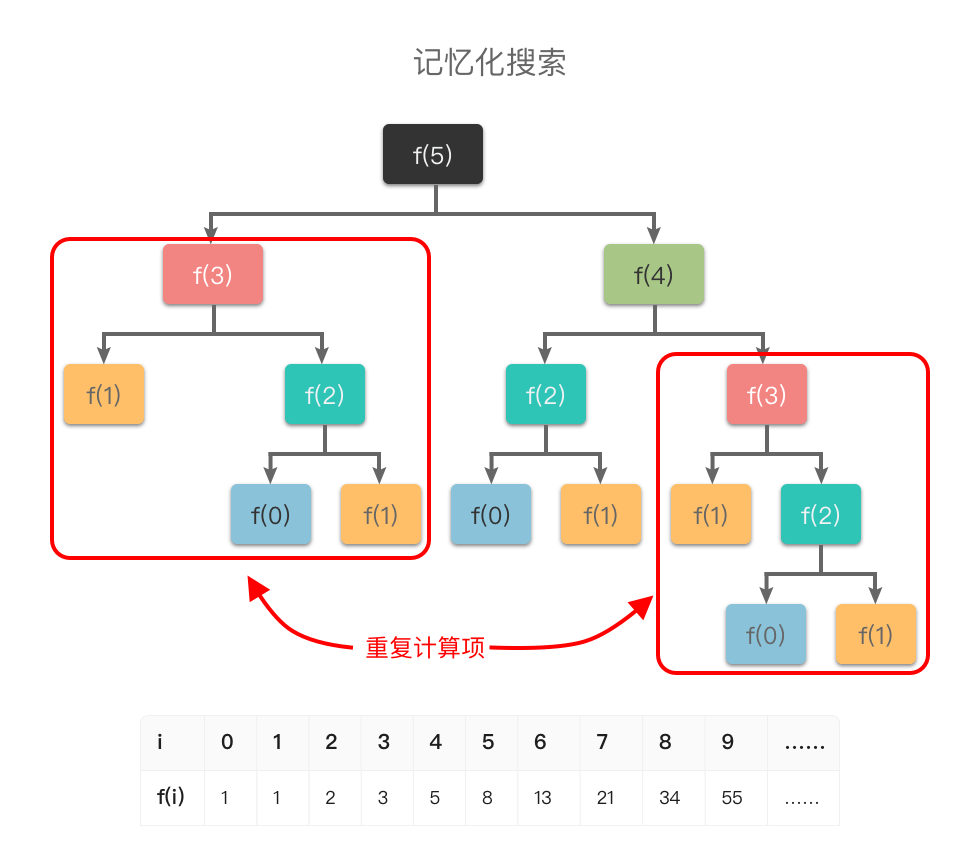
从图中可以看出：如果使用普通递归算法，想要计算 f(5)，需要先计算 f(3) 和 f(4)，而在计算 f(4) 时还需要计算 f(3)。这样 f(3) 就进行了多次计算，同理 f(0)、f(1)、f(2) 都进行了多次计算，从而导致了重复计算问题。

为了避免重复计算，在递归的同时，我们可以使用一个缓存（数组或哈希表）来保存已经求解过的 f(k) 的结果。如上图所示，当递归调用用到 f(k)时，先查看一下之前是否已经计算过结果，如果已经计算过，则直接从缓存中取值返回，而不用再递推下去，这样就避免了重复计算问题。

使用「记忆化搜索」方法解决斐波那契数列的代码如下：

public int fib(int n) {
    // 使用数组保存已经求解过的 f(k) 的结果
    int[] memo = new int[n + 1];
    Arrays.fill(memo, 0);
    return myFib(n, memo);
}

public int myFib(int n, int[] memo) {
    if (n == 0) {
        return 0;
    }
    if (n == 1) {
        return 1;
  
    // 已经计算过结果
    if (memo[n] != 0) {
        return memo[n];
  
    // 没有计算过结果
    memo[n] = myFib(n - 1, memo) + myFib(n - 2, memo);
    return memo[n];
}

2. 记忆化搜索与递推区别

「记忆化搜索」与「递推」都是动态规划的实现方式，但是两者之间有一些区别。

记忆化搜索：「自顶向下」的解决问题，采用自然的递归方式编写过程，在过程中会保存每个子问题的解（通常保存在一个数组或哈希表中）来避免重复计算。

优点：代码清晰易懂，可以有效的处理一些复杂的状态转移方程。有些状态转移方程是非常复杂的，使用记忆化搜索可以将复杂的状态转移方程拆分成多个子问题，通过递归调用来解决。

缺点：可能会因为递归深度过大而导致栈溢出问题。

递推：「自底向上」的解决问题，采用循环的方式编写过程，在过程中通过保存每个子问题的解（通常保存在一个数组或哈希表中）来避免重复计算。

优点：避免了深度过大问题，不存在栈溢出问题。计算顺序比较明确，易于实现。

缺点：无法处理一些复杂的状态转移方程。有些状态转移方程非常复杂，如果使用递推方法来计算，就会导致代码实现变得非常困难。

根据记忆化搜索和递推的优缺点，我们可以在不同场景下使用这两种方法。

适合使用「记忆化搜索」的场景：

问题的状态转移方程比较复杂，递推关系不是很明确。
问题适合转换为递归形式，并且递归深度不会太深。

适合使用「递推」的场景：

问题的状态转移方程比较简单，递归关系比较明确。
问题不太适合转换为递归形式，或者递归深度过大容易导致栈溢出。

3. 记忆化搜索解题步骤

我们在使用记忆化搜索解决问题的时候，其基本步骤如下：

写出问题的动态规划「状态」和「状态转移方程」。
定义一个缓存（数组或哈希表），用于保存子问题的解。
定义一个递归函数，用于解决问题。在递归函数中，首先检查缓存中是否已经存在需要计算的结果，如果存在则直接返回结果，否则进行计算，并将结果存储到缓存中，再返回结果。
在主函数中，调用递归函数并返回结果。

4. 记忆化搜索的应用

4.1 目标和

4.1.1 题目链接

494. 目标和 - 力扣open in new window

4.1.2 题目大意

描述：给定一个整数数组 nums 和一个整数 target。数组长度不超过 20。向数组中每个整数前加 + 或 -。然后串联起来构造成一个表达式。

要求：返回通过上述方法构造的、运算结果等于 target 的不同表达式数目。

说明：

1≤nums.length≤20。
0≤nums[i]≤10000 。
0≤sum(nums[i])≤10000。
−1000≤target≤1000 。

示例：

示例 1：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

1 2	输入：nums = [1], target = 1 输出：1

4.1.3 解题思路

思路 1：深度优先搜索（超时）

使用深度优先搜索对每位数字进行 + 或者 -，具体步骤如下：

定义从位置 0、和为 0 开始，到达数组尾部位置为止，和为 target 的方案数为 dfs(0, 0)。
下面从位置 0、和为 0 开始，以深度优先搜索遍历每个位置。
如果当前位置i到达最后一个位置size：
1. 如果和 cur_sum 等于目标和 target，则返回方案数 1。
2. 如果和 cur_sum 不等于目标和 target，则返回方案数 0。
递归搜索 i+1 位置，和为 cur_sum - nums[i] 的方案数。
递归搜索 i+1 位置，和为 cur_sum + nums[i] 的方案数。
将 4 ~ 5 两个方案数加起来就是当前位置 i、和为 cur_sum 的方案数，返回该方案数。
最终方案数为 dfs(0, 0)，将其作为答案返回即可。

思路 1：代码

public int findTargetSumWays(int[] nums, int target) {
      int size = nums.length;
      return dfs(0, 0, nums, target);
} 
private int dfs(int i, int curSum, int[] nums, int target) {
    if (i == nums.length) {
        if (curSum == target) {
            return 1;
        } else {
            return 0;
        }
    
    int ways1 = dfs(i + 1, curSum - nums[i], nums, target);
    int ways2 = dfs(i + 1, curSum + nums[i], nums, target)
    return ways1 + ways2;
}

思路 1：复杂度分析

时间复杂度：O(2ⁿ)。其中 n 为数组 nums 的长度。
空间复杂度：O(n)。递归调用的栈空间深度不超过 n。

思路 2：记忆化搜索

在思路 1 中我们单独使用深度优先搜索对每位数字进行 + 或者 - 的方法超时了。所以我们考虑使用记忆化搜索的方式，避免进行重复搜索。

这里我们使用哈希表 table 记录遍历过的位置 i 及所得到的的当前和cur_sum 下的方案数，来避免重复搜索。具体步骤如下：

定义从位置 0、和为 0 开始，到达数组尾部位置为止，和为 target 的方案数为 dfs(0, 0)。
下面从位置 0、和为 0 开始，以深度优先搜索遍历每个位置。
如果当前位置i遍历完所有位置：
1. 如果和 cur_sum 等于目标和 target，则返回方案数 1。
2. 如果和 cur_sum 不等于目标和 target，则返回方案数 0。
如果当前位置 i、和为 cur_sum 之前记录过（即使用 table 记录过对应方案数），则返回该方案数。
如果当前位置i、和为cur_sum之前没有记录过，则：
1. 递归搜索 i+1 位置，和为 cur_sum - nums[i] 的方案数。
2. 递归搜索 i+1 位置，和为 cur_sum + nums[i] 的方案数。
3. 将上述两个方案数加起来就是当前位置 i、和为 cur_sum 的方案数，将其记录到哈希表 table 中，并返回该方案数。
最终方案数为 dfs(0, 0)，将其作为答案返回即可。

思路 2：代码

public int findTargetSumWays(int[] nums, int target) {
       int size = nums.length;
       Map<String, Integer> table = new HashMap<>();
       return dfs(nums, 0, 0, target, table);
}
private int dfs(int[] nums, int i, int curSum, int target, Map<String, Integer> table) {
       if (i == nums.length) {
           return curSum == target ? 1 : 0;
       }
       String key = i + "," + curSum;
       if (table.containsKey(key)) {
           return table.get(key);
       }
       int count = dfs(nums, i + 1, curSum + nums[i], target, table)
                 + dfs(nums, i + 1, curSum - nums[i], target, table);
       table.put(key, count);
       return count;
}

思路 2：复杂度分析

时间复杂度：O(2ⁿ)。其中 n 为数组 nums 的长度。
空间复杂度：O(n)。递归调用的栈空间深度不超过 n。

4.2 第 N 个泰波那契数

4.2.1 题目链接

1137. 第 N 个泰波那契数 - 力扣open in new window

4.2.2 题目大意

描述：给定一个整数 n。

要求：返回第 n 个泰波那契数。

说明：

泰波那契数：T₀=0,T₁=1,T₂=1，且在 n>=0 的条件下，T_n+3=T_n+T_n+1+T_n+2。
0≤n≤370。
答案保证是一个 32 位整数，即 answer≤2³¹−1。

示例：

示例 1：

输入：n = 4
输出：4
解释：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

示例 2：

1 2	输入：n = 25 输出：1389537

4.2.3 解题思路

思路 1：记忆化搜索

问题的状态定义为：第 n 个泰波那契数。其状态转移方程为：T₀=0,T₁=1,T₂=1，且在 n>=0 的条件下，T_n+3=T_n+T_n+1+T_n+2。
定义一个长度为 n+1 数组 memo 用于保存一斤个计算过的泰波那契数。
定义递归函数my_tribonacci(n, memo)。
1. 当 n=0 或者 n=1，或者 n=2 时直接返回结果。
2. 当n>2时，首先检查是否计算过T(n)，即判断memo[n]是否等于0。
  1. 如果 memo[n]≠0，说明已经计算过 T(n)，直接返回 memo[n]。
  2. 如果 memo[n]=0，说明没有计算过 T(n)，则递归调用 my_tribonacci(n - 3, memo)、my_tribonacci(n - 2, memo)、my_tribonacci(n - 1, memo)，并将计算结果存入 memo[n]中，并返回 memo[n]。

思路 1：代码

public int tribonacci(int n) {
    // 使用数组保存已经求解过的 T(k) 的结果
    int[] memo = new int[n + 1];
    Arrays.fill(memo, 0);
    return myTribonacci(n, memo);
}

public int myTribonacci(int n, int[] memo) {
    if (n == 0) {
        return 0;
    }
    if (n == 1 || n == 2) {
        return 1;
  
    if (memo[n] != 0) {
        return memo[n];
  
    memo[n] = myTribonacci(n - 3, memo) + myTribonacci(n - 2, memo) + myTribonacci(n - 1, memo);
    return memo[n];
}

思路 1：复杂度分析

时间复杂度：O(n)。
空间复杂度：O(n)。