算法：线性DP基础知识

1. 线性动态规划简介

线性动态规划：具有「线性」阶段划分的动态规划方法统称为线性动态规划（简称为「线性 DP」），如下图所示。

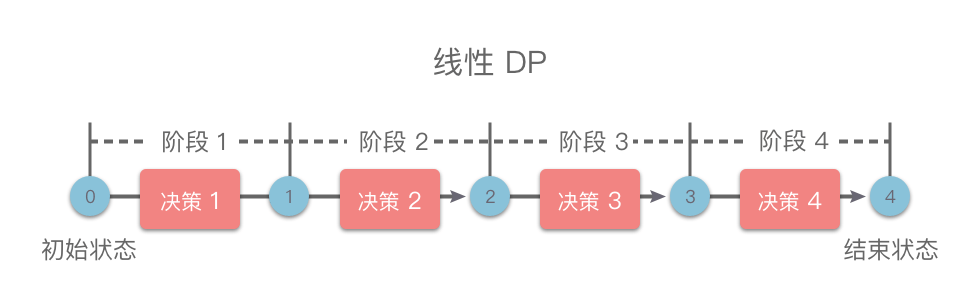
如果状态包含多个维度，但是每个维度上都是线性划分的阶段，也属于线性 DP。比如背包问题、区间 DP、数位 DP 等都属于线性 DP。

线性 DP 问题的划分方法有多种方式。

如果按照「状态的维度数」进行分类，我们可以将线性 DP 问题分为：一维线性 DP 问题、二维线性 DP 问题，以及多维线性 DP 问题。
如果按照「问题的输入格式」进行分类，我们可以将线性 DP 问题分为：单串线性 DP 问题、双串线性 DP 问题、矩阵线性 DP 问题，以及无串线性 DP 问题。

本文中，我们将按照问题的输入格式进行分类，对线性 DP 问题中各种类型问题进行一一讲解。

2. 单串线性 DP 问题

单串线性 DP 问题：问题的输入为单个数组或单个字符串的线性 DP 问题。状态一般可定义为 dp[i]，表示为：

「以数组中第 i个位置元素 nums[i] 为结尾的子数组（nums[0]…nums[i]）」的相关解。

「以数组中第 i−1 个位置元素 nums[i−1]为结尾的子数组（nums[0]…nums[i−1]）的相关解。

「以数组中前 i 个元素为子数组（nums[0]…nums[i−1]）的相关解。

这 3 种状态的定义区别在于相差一个元素 nums[i]。

第 1 种状态：子数组的长度为 i+1，子数组长度不可为空；
第 2 种状态、第 3 种状态：这两种状态描述是相同的。子数组的长度为 i，子数组长度可为空。在 i=0 时，方便用于表示空数组（以数组中前 0 个元素为子数组）。

2.1 最长递增子序列

单串线性 DP 问题中最经典的问题就是「最长递增子序列（Longest Increasing Subsequence，简称 LIS）」。

2.1.1 题目链接

300. 最长递增子序列 - 力扣open in new window

2.1.2 题目大意

描述：给定一个整数数组 nums。

要求：找到其中最长严格递增子序列的长度。

说明：

子序列：由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7]是数组 [0,3,1,6,2,2,7] 的子序列。
1≤nums.length≤2500。
−10⁴≤nums[i]≤10⁴。

示例：

示例 1：

1
2
3

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4。

示例 2：

1 2	输入：nums = [0,1,0,3,2,3] 输出：4

2.1.3 解题思路

思路 1：动态规划

1. 划分阶段

按照子序列的结尾位置进行阶段划分。

2. 定义状态

定义状态 dp[i] 表示为：以 nums[i] 结尾的最长递增子序列长度。

3. 状态转移方程

一个较小的数后边如果出现一个较大的数，则会形成一个更长的递增子序列。

对于满足 0≤j<i 的数组元素 nums[j] 和 nums[i] 来说：

如果 nums[j]<nums[i]，则 nums[i]可以接在 nums[j]后面，此时以 nums[i]结尾的最长递增子序列长度会在「以 nums[j]结尾的最长递增子序列长度」的基础上加 1，即：dp[i]=dp[j]+1。
如果 nums[i]≤nums[j]，则 nums[i]不可以接在 nums[j]后面，可以直接跳过。

综上，我们的状态转移方程为：

**dp[i]=max(dp[i],dp[j]+1),0≤j<i,nums[j]<nums[i]**。

4. 初始条件

默认状态下，把数组中的每个元素都作为长度为 1 的递增子序列。即 dp[i]=1。

5. 最终结果

根据我们之前定义的状态，dp[i] 表示为：以 nums[i] 结尾的最长递增子序列长度。那为了计算出最大的最长递增子序列长度，则需要再遍历一遍 dp 数组，求出最大值即为最终结果。

思路 1：动态规划代码

public int lengthOfLIS(int[] nums) {
     int size = nums.length;
     int[] dp = new int[size];
     Arrays.fill(dp, 1)
     for (int i = 0; i < size; i++) {
         for (int j = 0; j < i; j++) {
             if (nums[i] > nums[j]) {
                 dp[i] = Math.max(dp[i], dp[j] + 1);
             }
         }
     }
     int maxLength = Arrays.stream(dp).max().orElse(0);
     return maxLength;
 }

思路 1：复杂度分析

时间复杂度：O(n²)。两重循环遍历的时间复杂度是 O(n²)，最后求最大值的时间复杂度是 O(n)，所以总体时间复杂度为 O(n²)。
空间复杂度：O(n)。用到了一维数组保存状态，所以总体空间复杂度为 O(n)。

2.2 最大子数组和

单串线性 DP 问题中除了子序列相关的线性 DP 问题，还有子数组相关的线性 DP 问题。

注意：

子序列：由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。

子数组：指的是数组中的一个连续子序列。

「子序列」与「子数组」都可以看做是原数组的一部分，而且都不会改变原来数组中元素的相对顺序。其区别在于数组元素是否要求连续。

2.2.1 题目链接

53. 最大子数组和 - 力扣open in new window

2.2.2 题目大意

描述：给定一个整数数组 nums。

要求：找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

说明：

子数组：指的是数组中的一个连续部分。
1≤nums.length≤10⁵。
−10⁴ ≤ nums[i]≤10⁴。

示例：

示例 1：

1
2
3

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6。

示例 2：

1 2	输入：nums = [1] 输出：1

2.2.3 解题思路

思路 1：动态规划

1. 划分阶段

按照连续子数组的结束位置进行阶段划分。

2. 定义状态

定义状态 dp[i] 为：以第 i 个数结尾的连续子数组的最大和。

3. 状态转移方程

状态 dp[i] 为：以第 i 个数结尾的连续子数组的最大和。则我们可以从「第 i−1 个数结尾的连续子数组的最大和」，以及「第 i 个数的值」来讨论 dp[i]。

如果 dp[i−1]<0，则「第 i−1 个数结尾的连续子数组的最大和」+「第 i 个数的值」<「第 i 个数的值」，即：dp[i−1]+nums[i]<nums[i]。所以，此时 dp[i] 应取「第 i 个数的值」，即 dp[i]=nums[i]。
如果 dp[i−1]≥0，则「第 i−1 个数结尾的连续子数组的最大和」 +「第 i 个数的值」 >= 第 i 个数的值，即：dp[i−1]+nums[i]≥nums[i]。所以，此时 dp[i] 应取「第 i−1 个数结尾的连续子数组的最大和」+「第 i 个数的值」，即 dp[i]=dp[i−1]+nums[i]。

归纳一下，状态转移方程为：

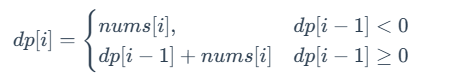
4. 初始条件

第 0 个数结尾的连续子数组的最大和为 nums[0]，即 dp[0]=nums[0]。

5. 最终结果

根据状态定义，dp[i] 为：以第 i 个数结尾的连续子数组的最大和。则最终结果应为所有 dp[i] 的最大值，即 max(dp)。

思路 1：代码

public int maxSubArray(int[] nums) {
        int size = nums.length;
        int[] dp = new int[size];

        dp[0] = nums[0];
        for (int i = 1; i < size; i++) {
            if (dp[i - 1] < 0) {
                dp[i] = nums[i];
            } else {
                dp[i] = dp[i - 1] + nums[i];
            }
        }

        int maxSum = Arrays.stream(dp).max().orElse(0);
        return maxSum;
}

思路 1：复杂度分析

时间复杂度：O(n)，其中 n 为数组 nums的元素个数。
空间复杂度：O(n)。

思路 2：动态规划 + 滚动优化

因为 dp[i]只和 dp[i−1]和当前元素 nums[i]相关，我们也可以使用一个变量 subMax来表示以第 i 个数结尾的连续子数组的最大和。然后使用 ansMax来保存全局中最大值。

思路 2：代码

public int maxSubArray(int[] nums) {
        int size = nums.length;
        int subMax = nums[0];
        int ansMax = nums[0];

        for (int i = 1; i < size; i++) {
            if (subMax < 0) {
                subMax = nums[i];
            } else {
                subMax += nums[i];
            }
            ansMax = Math.max(ansMax, subMax);
        }
        return ansMax;
}

思路 2：复杂度分析

时间复杂度：O(n)，其中 n 为数组 nums 的元素个数。
空间复杂度：O(1)。

2.3 最长的斐波那契子序列的长度

有一些单串线性 DP 问题在定义状态时需要考虑两个结束位置，只考虑一个结束位置的无法清楚描述问题。这时候我们就需要需要增加一个结束位置维度来定义状态。

2.3.1 题目链接

873. 最长的斐波那契子序列的长度 - 力扣open in new window

2.3.2 题目大意

描述：给定一个严格递增的正整数数组 arr。

要求：从数组 arr 中找出最长的斐波那契式的子序列的长度。如果不存斐波那契式的子序列，则返回 0。

说明：

斐波那契式序列：如果序列 X₁,X₂,…,X_n 满足：
- n≥3；
- 对于所有 i+2≤n，都有 X_i+X_i+1=X_i+2。
则称该序列为斐波那契式序列。
斐波那契式子序列：从序列 A 中挑选若干元素组成子序列，并且子序列满足斐波那契式序列，则称该序列为斐波那契式子序列。例如：A=[3,4,5,6,7,8]。则 [3,5,8] 是 A 的一个斐波那契式子序列。
3≤arr.length≤1000。
1≤arr[i]<arr[i+1]≤10⁹。

示例：

示例 1：

1
2
3

输入: arr = [1,2,3,4,5,6,7,8]
输出: 5
解释: 最长的斐波那契式子序列为 [1,2,3,5,8]。

示例 2：

1
2
3

输入: arr = [1,3,7,11,12,14,18]
输出: 3
解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18]。

2.3.3 解题思路

思路 1：暴力枚举（超时）

假设 arr[i]、arr[j]、arr[k]是序列 arr中的 3 个元素，且满足关系：arr[i]+arr[j]==arr[k]，则 arr[i]、arr[j]、arr[k]就构成了 arr 的一个斐波那契式子序列。

通过 arr[i]、arr[j]，我们可以确定下一个斐波那契式子序列元素的值为 arr[i]+arr[j]。

因为给定的数组是严格递增的，所以对于一个斐波那契式子序列，如果确定了 arr[i]、arr[j]，则可以顺着 arr 序列，从第 j+1 的元素开始，查找值为 arr[i]+arr[j]的元素。找到 arr[i]+arr[j] 之后，然后再顺着查找子序列的下一个元素。

简单来说，就是确定了 arr[i]、arr[j]，就能尽可能的得到一个长的斐波那契式子序列，此时我们记录下子序列长度。然后对于不同的 arr[i]、arr[j]，统计不同的斐波那契式子序列的长度。

最后将这些长度进行比较，其中最长的长度就是答案。

思路 1：代码

 public int lenLongestFibSubseq(int[] arr) {
        int size = arr.length;
        int ans = 0;

        for (int i = 0; i < size; i++) {
            for (int j = i + 1; j < size; j++) {
                int tempAns = 0;
                int tempI = i;
                int tempJ = j;
                int k = j + 1;

                while (k < size) {
                    if (arr[tempI] + arr[tempJ] == arr[k]) {
                        tempAns += 1;
                        tempI = tempJ;
                        tempJ = k;
                    }
                    k += 1;
                }

                if (tempAns > ans) {
                    ans = tempAns;
                }
            }
        }

        if (ans > 0) {
            return ans + 2;
        } else {
            return ans;
        }
}

思路 1：复杂度分析

时间复杂度：O(n³)，其中 n 为数组 arr 的元素个数。
空间复杂度：O(1)。

思路 2：哈希表

对于 arr[i]、arr[j]，要查找的元素 arr[i]+arr[j]是否在 arr中，我们可以预先建立一个反向的哈希表。键值对关系为 value:idx，这样就能在 O(1)的时间复杂度通过 arr[i]+arr[j]的值查找到对应的 arr[k]，而不用像原先一样线性查找 arr[k]了。

思路 2：代码

public int lenLongestFibSubseq(int[] arr) {
        int size = arr.length;
        int ans = 0;
        Map<Integer, Integer> idxMap = new HashMap<>();

        for (int idx = 0; idx < size; idx++) {
            idxMap.put(arr[idx], idx);
        }

        for (int i = 0; i < size; i++) {
            for (int j = i + 1; j < size; j++) {
                int tempAns = 0;
                int tempI = i;
                int tempJ = j;

                while (idxMap.containsKey(arr[tempI] + arr[tempJ])) {
                    tempAns += 1;
                    int k = idxMap.get(arr[tempI] + arr[tempJ]);
                    tempI = tempJ;
                    tempJ = k;
                }

                if (tempAns > ans) {
                    ans = tempAns;
                }
            }
        }

        if (ans > 0) {
            return ans + 2;
        } else {
            return ans;
        }
}

思路 2：复杂度分析

时间复杂度：O(n²)，其中 n 为数组 arr 的元素个数。
空间复杂度：O(n)。

思路 3：动态规划 + 哈希表

1. 划分阶段

按照斐波那契式子序列相邻两项的结尾位置进行阶段划分。

2. 定义状态

定义状态 dp[i] [j]表示为：以 arr[i]、arr[j]为结尾的斐波那契式子序列的最大长度。

3. 状态转移方程

4. 初始条件

默认状态下，数组中任意相邻两项元素都可以作为长度为 2 的斐波那契式子序列，即 dp[i] [j]=2。

5. 最终结果

根据我们之前定义的状态，dp[i] [j]表示为：以 arr[i]、arr[j]为结尾的斐波那契式子序列的最大长度。那为了计算出最大的最长递增子序列长度，则需要在进行状态转移时，求出最大值 ans 即为最终结果。

因为题目定义中，斐波那契式中 n≥3，所以只有当 ans≥3 时，返回 ans。如果 ans<3，则返回 0。

注意：在进行状态转移的同时，我们应和「思路 2：哈希表」一样采用哈希表优化的方式来提高效率，降低算法的时间复杂度。

思路 3：代码

public int lenLongestFibSubseq(int[] arr) {
        int size = arr.length;
        int[][] dp = new int[size][size];
        int ans = 0;

        // 初始化 dp
        for (int i = 0; i < size; i++) {
            for (int j = i + 1; j < size; j++) {
                dp[i][j] = 2;
            }
        }

        Map<Integer, Integer> idxMap = new HashMap<>();
        // 将 value : idx 映射为哈希表，这样可以快速通过 value 获取到 idx
        for (int idx = 0; idx < size; idx++) {
            idxMap.put(arr[idx], idx);
        }

        for (int i = 0; i < size; i++) {
            for (int j = i + 1; j < size; j++) {
                if (idxMap.containsKey(arr[i] + arr[j])) {
                    // 获取 arr[i] + arr[j] 的 idx，即斐波那契式子序列下一项元素
                    int k = idxMap.get(arr[i] + arr[j]);

                    dp[j][k] = Math.max(dp[j][k], dp[i][j] + 1);
                    ans = Math.max(ans, dp[j][k]);
                }
            }
        }

        if (ans >= 3) {
            return ans;
        }
        return 0;
}

思路 3：复杂度分析

时间复杂度：O(n²)，其中 n 为数组 arr的元素个数。
空间复杂度：O(n)。

3. 双串线性 DP 问题

双串线性 DP 问题：问题的输入为两个数组或两个字符串的线性 DP 问题。状态一般可定义为 dp[i] [j]，表示为：

「以第一个数组中第 i个位置元素 nums1[i] 为结尾的子数组（nums1[0]…nums1[i]）」与「以第二个数组中第 j 个位置元素 nums2[j]为结尾的子数组（nums2[0]…nums2[j]）」的相关解。

「以第一个数组中第 i−1个位置元素 nums1[i−1]为结尾的子数组（nums1[0]…nums1[i−1]」与「以第二个数组中第 j−1个位置元素 nums2[j−1] 为结尾的子数组（nums2[0]…nums2[j−1]）」的相关解。

「以第一个数组中前 i 个元素为子数组（nums1[0]…nums1[i−1]」与「以第二个数组中前 j 个元素为子数组（nums2[0]…nums2[j−1]」的相关解。

这 3 种状态的定义区别在于相差一个元素 nums1[i]或 nums2[j]。

第 1 种状态：子数组的长度为 i+1或 j+1，子数组长度不可为空
第 2 种状态、第 3 种状态：子数组的长度为 i 或 j，子数组长度可为空。i=0或 j=0时，方便用于表示空数组（以数组中前 0 个元素为子数组）。

3.1 最长公共子序列

双串线性 DP 问题中最经典的问题就是「最长公共子序列（Longest Common Subsequence，简称 LCS）」。

3.1.1 题目链接

1143. 最长公共子序列 - 力扣open in new window

3.1.2 题目大意

描述：给定两个字符串 text1 和 text2。

要求：返回两个字符串的最长公共子序列的长度。如果不存在公共子序列，则返回 0。

说明：

子序列：原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
公共子序列：两个字符串所共同拥有的子序列。
1≤text1.length,text2.length≤1000。
text1 和 text2仅由小写英文字符组成。

示例：

示例 1：

1
2
3

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace"，它的长度为 3。

示例 2：

1
2
3

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc"，它的长度为 3。

3.1.3 解题思路

思路 1：动态规划

1. 划分阶段

按照两个字符串的结尾位置进行阶段划分。

2. 定义状态

定义状态 dp[i] [j]表示为：「以 text1 中前 i 个元素组成的子字符串 str1 」与「以 text2 中前 j 个元素组成的子字符串 str2」的最长公共子序列长度为 dp[i] [j]。

3. 状态转移方程

双重循环遍历字符串 text1 和 text2，则状态转移方程为：

4. 初始条件

当 i=0 时，str1 表示的是空串，空串与 str2 的最长公共子序列长度为 0，即 dp[0] [j]=0。
当 j=0 时，str2 表示的是空串，str1 与空串的最长公共子序列长度为 0，即dp[i] [0]=0。

5. 最终结果

根据状态定义，最后输出 dp[sise1] [size2]（即 text1 与 text2 的最长公共子序列长度）即可，其中 size1、size2 分别为 text1、text2 的字符串长度。

思路 1：代码

public int longestCommonSubsequence(String text1, String text2) {
        int size1 = text1.length();
        int size2 = text2.length();
        int[][] dp = new int[size1 + 1][size2 + 1];

        for (int i = 1; i <= size1; i++) {
            for (int j = 1; j <= size2; j++) {
                if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }

        return dp[size1][size2];
}

思路 1：复杂度分析

时间复杂度：O(n×m)，其中 n、m 分别是字符串 text1、text2 的长度。两重循环遍历的时间复杂度是 O(n×m)，所以总的时间复杂度为 O(n×m)。
空间复杂度：O(n×m)。用到了二维数组保存状态，所以总体空间复杂度为 O(n×m)。

3.2 最长重复子数组

3.2.1 题目链接

718. 最长重复子数组 - 力扣open in new window

3.2.2 题目大意

描述：给定两个整数数组 nums1、nums2。

要求：计算两个数组中公共的、长度最长的子数组长度。

说明：

1≤nums1.length,nums2.length≤1000。
0≤nums1[i],nums2[i]≤100。

示例：

示例 1：

1
2
3

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

1 2	输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0] 输出：5

3.2.3 解题思路

思路 1：动态规划

1. 划分阶段

按照子数组结尾位置进行阶段划分。

2. 定义状态

定义状态 dp[i] [j]为：「以 nums1中前 i 个元素为子数组（nums1[0]…nums2[i−1]）」和「以 nums2 中前 j 个元素为子数组（nums2[0]…nums2[j−1]）」的最长公共子数组长度。

3. 状态转移方程

如果 nums1[i−1]=nums2[j−1]，则当前元素可以构成公共子数组，此时 dp[i] [j]= dp[i-1] [j-1]+1。
如果 nums1[i−1]≠nums2[j−1]，则当前元素不能构成公共子数组，此时 dp[i] [j]=0。

4. 初始条件

当 i=0 时，nums1[0]…nums1[i−1]表示的是空数组，空数组与 nums2[0]…nums2[j−1]的最长公共子序列长度为 0，即 dp[0] [j]=0。
当 j=0时，nums2[0]…nums2[j−1]表示的是空数组，空数组与 nums1[0]…nums1[i−1]的最长公共子序列长度为 0，即 dp[i] [0]=0。

5. 最终结果

根据状态定义，dp[i] [j]为：「以 nums1中前 i 个元素为子数组（nums1[0]…nums2[i−1]）和「以 nums2 中前 j 个元素为子数组（nums2[0]…nums2[j−1]）的最长公共子数组长度。在遍历过程中，我们可以使用 res 记录下所有 dp[i] [j]中最大值即为答案。

思路 1：代码

public int findLength(int[] nums1, int[] nums2) {
        int size1 = nums1.length;
        int size2 = nums2.length;
        int[][] dp = new int[size1 + 1][size2 + 1];
        int res = 0;

        for (int i = 1; i <= size1; i++) {
            for (int j = 1; j <= size2; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > res) {
                    res = dp[i][j];
                }
            }
        }
        return res;
}

思路 1：复杂度分析

时间复杂度：O(n×m)。其中 n 是数组 nums1 的长度，m 是数组 nums2的长度。
空间复杂度：O(n×m)。

3.3 编辑距离

双串线性 DP 问题中除了经典的最长公共子序列问题之外，还包括字符串的模糊匹配问题。

3.3.1 题目链接

72. 编辑距离 - 力扣open in new window

3.3.2 题目大意

描述：给定两个单词 word1、word2。

对一个单词可以进行以下三种操作：

插入一个字符
删除一个字符
替换一个字符

要求：计算出将 word1 转换为 word2所使用的最少操作数。

说明：

0≤word1.length,word2.length≤500。
word1 和 word2 由小写英文字母组成。

示例：

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

3.3.3 解题思路

思路 1：动态规划

1. 划分阶段

按照两个字符串的结尾位置进行阶段划分。

2. 定义状态

定义状态 dp[i] [j]表示为：「以 word1中前 i 个字符组成的子字符串 str1」变为「以 word2 中前 j 个字符组成的子字符串 str2」，所需要的最少操作次数。

3. 状态转移方程

综合上述情况，状态转移方程为：

4. 初始条件

当 i=0，「以 word1 中前 0 个字符组成的子字符串 str1」为空字符串，「str1」变为「以 word2 中前 j 个字符组成的子字符串 str2」时，至少需要插入 j 次，即：dp[0] [j]=j。
当 j=0，「以 word2中前 0 个字符组成的子字符串 str2」为空字符串，「以 word1中前 i 个字符组成的子字符串 str1」变为「str2」时，至少需要删除 i 次，即：dp[i] [0]=i。

5. 最终结果

根据状态定义，最后输出 dp[size] [size]（即 word1变为 word2所使用的最少操作数）即可。其中 size1、size2 分别为 word1、word2 的字符串长度。

思路 1：代码

 public int minDistance(String word1, String word2) {
        int size1 = word1.length();
        int size2 = word2.length();
        int[][] dp = new int[size1 + 1][size2 + 1];

        for (int i = 0; i <= size1; i++) {
            dp[i][0] = i;
        }
        for (int j = 0; j <= size2; j++) {
            dp[0][j] = j;
        }

        for (int i = 1; i <= size1; i++) {
            for (int j = 1; j <= size2; j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]) + 1;
                }
            }
        }

        return dp[size1][size2];
}

思路 1：复杂度分析

时间复杂度：O(n×m)，其中 n、m分别是字符串 word1、word2 的长度。两重循环遍历的时间复杂度是 O(n×m)，所以总的时间复杂度为 O(n×m)。
空间复杂度：O(n×m)。用到了二维数组保存状态，所以总体空间复杂度为 O(n×m)。

1
2
3

5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

1 2	输入：grid = [[1,2,3],[4,5,6]] 输出：12

4.矩阵线性 DP问题

矩阵线性 DP 问题：问题的输入为二维矩阵的线性 DP 问题。状态一般可定义为 dp[i] [j]，表示为：从「位置 (0,0)」到达「位置 (i,j)」的相关解。

4.1 最小路径和

4.1.1 题目链接

64. 最小路径和 - 力扣open in new window

4.1.2 题目大意

描述：给定一个包含非负整数的 m×n 大小的网格 grid。

要求：找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：

每次只能向下或者向右移动一步。
m==grid.length。
n==grid[i].length。
1≤m,n≤200。
0≤grid[i] [j]≤100。

示例：

示例 1：

1
2
3

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

1 2	输入：grid = [[1,2,3],[4,5,6]] 输出：12

4.1.3 解题思路

思路 1：动态规划

1. 划分阶段

按照路径的结尾位置（行位置、列位置组成的二维坐标）进行阶段划分。

2. 定义状态

定义状态 dp[i] [j]为：从位置 (0,0)到达位置 (i,j) 的最小路径和。

3. 状态转移方程

当前位置 (i,j) 只能从左侧位置 (i,j−1) 或者上方位置 (i−1,j) 到达。为了使得从左上角到达 (i,j)位置的最小路径和最小，应从 (i,j−1) 位置和 (i−1,j) 位置选择路径和最小的位置达到 (i,j)。

即状态转移方程为：dp[i] [j]=min(dp[i] [j-1],dp[i-1] [j])+grid[i] [j] 。

4. 初始条件

当左侧和上方是矩阵边界时（即 i=0,j=0），dp[i] [j]=grid[i] [j]。
当只有左侧是矩阵边界时（即 i≠0,j=0），只能从上方到达，dp[i] [j]=dp[i-1] [j]+grid[i] [j] 。
当只有上方是矩阵边界时（即 i=0,j≠0），只能从左侧到达，dp[i] [j]=dp[i] [j-1]+grid[i] [j] 。

5. 最终结果

根据状态定义，最后输出 dp[rows−1] [cols−1]（即从左上角到达 (rows−1,cols−1)(rows - 1, cols - 1)位置的最小路径和）即可。其中 rows、cols 分别为 grid 的行数、列数。

思路 1：代码

public int minPathSum(int[][] grid) {
        int rows = grid.length;
        int cols = grid[0].length;
        int[][] dp = new int[rows][cols];

        dp[0][0] = grid[0][0];

        // 初始化第一列
        for (int i = 1; i < rows; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }

        // 初始化第一行
        for (int j = 1; j < cols; j++) {
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }

        // 填充dp数组
        for (int i = 1; i < rows; i++) {
            for (int j = 1; j < cols; j++) {
                dp[i][j] = Math.min(dp[i][j - 1], dp[i - 1][j]) + grid[i][j];
            }
        }

        return dp[rows - 1][cols - 1];
}

思路 1：复杂度分析

时间复杂度：O(m∗n)，其中 m、n 分别为 grid 的行数和列数。
空间复杂度：O(m∗n)。

4.2 最大正方形

4.2.1 题目链接

221. 最大正方形 - 力扣open in new window

4.2.2 题目大意

描述：给定一个由 '0' 和 '1' 组成的二维矩阵 matrix。

要求：找到只包含 '1' 的最大正方形，并返回其面积。

说明：

m==matrix.length。
n==matrix[i].length。
1≤m,n≤300。
matrix[i] [j]为 '0' 或 '1'。

示例：

示例 1：

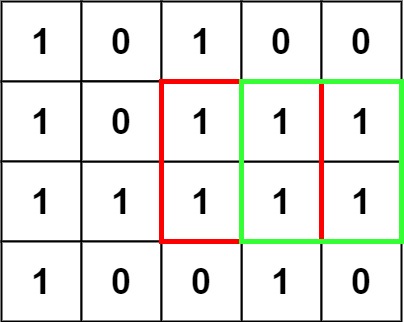
1 2	输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] 输出：4

示例 2：

1 2	输入：matrix = [["0","1"],["1","0"]] 输出：1

4.2.3 解题思路

思路 1：动态规划

1. 划分阶段

按照正方形的右下角坐标进行阶段划分。

2. 定义状态

定义状态 dp[i] [j] 表示为：以矩阵位置 (i,j) 为右下角，且值包含 1 的正方形的最大边长。

3. 状态转移方程

4. 初始条件

默认所有以矩阵位置 (i,j) 为右下角，且值包含 1 的正方形的最大边长都为 0，即 dp[i] [j] 。

5. 最终结果

根据我们之前定义的状态， dp[i] [j] 表示为：以矩阵位置 (i,j)为右下角，且值包含 1 的正方形的最大边长。则最终结果为所有 dp[i] [j]中的最大值。

思路 1：代码

 public int maximalSquare(char[][] matrix) {
        int rows = matrix.length;
        int cols = matrix[0].length;
        int maxSize = 0;
        int[][] dp = new int[rows + 1][cols + 1];

        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (matrix[i][j] == '1') {
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i][j - 1]) + 1;
                    }
                    maxSize = Math.max(maxSize, dp[i][j]);
                }
            }
        }

        return maxSize * maxSize;
}

思路 1：复杂度分析

时间复杂度：O(m×n)，其中 m、n 分别为二维矩阵 matrix 的行数和列数。
空间复杂度：O(m×n)。

5. 无串线性 DP 问题

无串线性 DP 问题：问题的输入不是显式的数组或字符串，但依然可分解为若干子问题的线性 DP 问题。

5.1 整数拆分

5.1.1 题目链接

343. 整数拆分 - 力扣open in new window

5.1.2 题目大意

描述：给定一个正整数 n，将其拆分为 k(k≥2) 个正整数的和，并使这些整数的乘积最大化。

要求：返回可以获得的最大乘积。

说明：

2≤n≤58。

示例：

示例 1：

1
2
3

输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2：

1
2
3

输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

5.1.3 解题思路

思路 1：动态规划

1. 划分阶段

按照正整数进行划分。

2. 定义状态

定义状态 dp[i]表示为：将正整数 i 拆分为至少 2 个正整数的和之后，这些正整数的最大乘积。

3. 状态转移方程

4. 初始条件

0 和 1 都不能被拆分，所以 dp[0]=0,dp[1]=0。

5. 最终结果

根据我们之前定义的状态，dp[i] 表示为：将正整数 i 拆分为至少 2 个正整数的和之后，这些正整数的最大乘积。则最终结果为 dp[n]。

思路 1：代码

 public int integerBreak(int n) {
        int[] dp = new int[n + 1];

        for (int i = 2; i <= n; i++) {
            for (int j = 1; j < i; j++) {
                dp[i] = Math.max(dp[i], Math.max((i - j) * j, dp[i - j] * j));
            }
        }

        return dp[n];
}

思路 1：复杂度分析

时间复杂度：O(n²)。
空间复杂度：O(n)。

5.2 只有两个键的键盘

5.2.1 题目链接

650. 只有两个键的键盘open in new window

5.2.2 题目大意

描述：最初记事本上只有一个字符 'A'。你每次可以对这个记事本进行两种操作：

Copy All（复制全部）：复制这个记事本中的所有字符（不允许仅复制部分字符）。
Paste（粘贴）：粘贴上一次复制的字符。

现在，给定一个数字 n，需要使用最少的操作次数，在记事本上输出恰好 n 个 'A' 。

要求：返回能够打印出 n 个 'A' 的最少操作次数。

说明：

1≤n≤1000。

示例：

示例 1：

输入：3
输出：3
解释
最初, 只有一个字符 'A'。
第 1 步, 使用 Copy All 操作。
第 2 步, 使用 Paste 操作来获得 'AA'。
第 3 步, 使用 Paste 操作来获得 'AAA'。

示例 2：

1 2	输入：n = 1 输出：0

5.2.3 解题思路

思路 1：动态规划

1. 划分阶段

按照字符 'A' 的个数进行阶段划分。

2. 定义状态

定义状态 dp[i] 表示为：通过「复制」和「粘贴」操作，得到 i 个字符 'A'，最少需要的操作数。

3. 状态转移方程

4. 初始条件

当 i=1时，最少需要的操作数为 0。所以 dp[1]=0。

5. 最终结果

根据我们之前定义的状态，dp[i]表示为：通过「复制」和「粘贴」操作，得到 i 个字符 'A'，最少需要的操作数。所以最终结果为 dp[n]。

思路 1：动态规划代码

public int minSteps(int n) {
        int[] dp = new int[n + 1];
        for (int i = 2; i <= n; i++) {
            dp[i] = Integer.MAX_VALUE;
            for (int j = 1; j <= Math.sqrt(i); j++) {
                if (i % j == 0) {
                    dp[i] = Math.min(dp[i], dp[j] + i / j, dp[i / j] + j);
                }
            }
        }
        return dp[n];
}

线性DP基础知识

1. 线性动态规划简介

2. 单串线性 DP 问题

2.1 最长递增子序列

2.1.1 题目链接

2.1.2 题目大意

2.1.3 解题思路

思路 1：动态规划

1. 划分阶段

2. 定义状态

3. 状态转移方程

4. 初始条件

5. 最终结果

思路 1：动态规划代码

思路 1：复杂度分析

2.2 最大子数组和

2.2.1 题目链接

2.2.2 题目大意

2.2.3 解题思路

思路 1：动态规划

1. 划分阶段

2. 定义状态

3. 状态转移方程

4. 初始条件

5. 最终结果

思路 1：代码

思路 1：复杂度分析

思路 2：动态规划 + 滚动优化

思路 2：代码

思路 2：复杂度分析

2.3 最长的斐波那契子序列的长度

2.3.1 题目链接

2.3.2 题目大意

2.3.3 解题思路

思路 1： 暴力枚举（超时）

思路 1：代码

思路 1：复杂度分析

思路 2：哈希表

思路 2：代码

思路 2：复杂度分析

思路 3：动态规划 + 哈希表

1. 划分阶段

2. 定义状态

3. 状态转移方程

4. 初始条件

5. 最终结果

思路 3：代码

思路 3：复杂度分析

3. 双串线性 DP 问题

3.1 最长公共子序列

3.1.1 题目链接

3.1.2 题目大意

3.1.3 解题思路

思路 1：动态规划

1. 划分阶段

2. 定义状态

3. 状态转移方程

4. 初始条件

5. 最终结果

思路 1：代码

思路 1：复杂度分析

3.2 最长重复子数组

3.2.1 题目链接

3.2.2 题目大意

3.2.3 解题思路

思路 1：动态规划

1. 划分阶段

2. 定义状态

3. 状态转移方程

4. 初始条件

5. 最终结果

思路 1：代码

思路 1：复杂度分析

3.3 编辑距离

3.3.1 题目链接

3.3.2 题目大意

3.3.3 解题思路

思路 1：动态规划

1. 划分阶段

2. 定义状态

思路 1：暴力枚举（超时）