1. 二叉搜索树简介

二叉搜索树（Binary Search Tree）：也叫做二叉查找树、有序二叉树或者排序二叉树。是指一棵空树或者具有下列性质的二叉树：

  • 如果任意节点的左子树不为空，则左子树上所有节点的值均小于它的根节点的值。
  • 如果任意节点的右子树不为空，则右子树上所有节点的值均大于它的根节点的值。
  • 任意节点的左子树、右子树均为二叉搜索树。

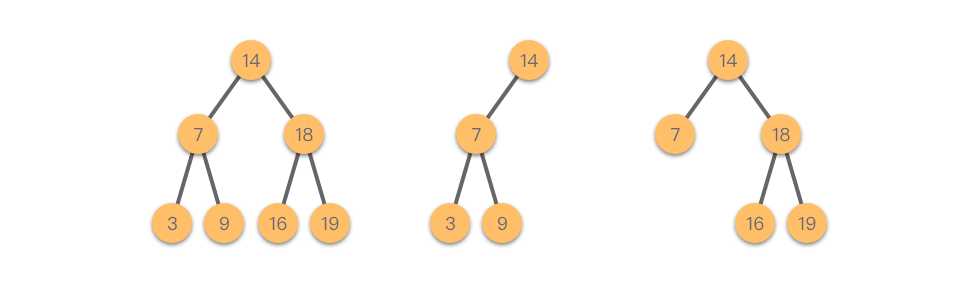
如图所示，这 3 棵树都是二叉搜索树。

二叉搜索树

二叉树具有一个特性，即：左子树的节点值 < 根节点值 < 右子树的节点值。

根据这个特性，如果我们以中序遍历的方式遍历整个二叉搜索树时，会得到一个递增序列。

2. 二叉搜索树的查找

二叉搜索树的查找：在二叉搜索树中查找值为 𝑣𝑎𝑙 的节点。

2.1 二叉搜索树的查找算法步骤

按照二叉搜索树的定义，在进行元素查找时，我们只需要根据情况判断需要往左还是往右走。这样，每次根据情况判断都会缩小查找范围，从而提高查找效率。二叉树的查找步骤如下：

  1. 如果二叉搜索树为空，则查找失败，结束查找，并返回空指针节点 𝑁𝑜𝑛𝑒。
  2. 如果二叉搜索树不为空，则将要查找的值𝑣𝑎𝑙与二叉搜索树根节点的值𝑟𝑜𝑜𝑡.𝑣𝑎𝑙进行比较：
    1. 如果 𝑣𝑎𝑙==𝑟𝑜𝑜𝑡.𝑣𝑎𝑙，则查找成功，结束查找，返回被查找到的节点。
    2. 如果 𝑣𝑎𝑙<𝑟𝑜𝑜𝑡.𝑣𝑎𝑙，则递归查找左子树。
    3. 如果 𝑣𝑎𝑙>𝑟𝑜𝑜𝑡.𝑣𝑎𝑙，则递归查找右子树。

2.2 二叉搜索树的查找代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}
public class Solution {  
    public TreeNode searchBST(TreeNode root, int val) {  
        if (root == null) {  
            return null;  
        }  
  
        if (val == root.val) {  
            return root;  
        } else if (val < root.val) {  
            return searchBST(root.left, val);  
        } else {  
            return searchBST(root.right, val);  
        }  
    }  
}

2.3 二叉搜索树的查找算法分析

  • 二叉搜索树的查找时间复杂度和树的形态有关。
  • 在最好情况下，二叉搜索树的形态与二分查找的判定树相似。每次查找都可以所辖一半搜索范围。查找路径最多从根节点到叶子节点，比较次数最多为树的高度 log⁡2𝑛。在最好情况下查找的时间复杂度为 𝑂(log⁡2𝑛)。
  • 在最坏情况下，二叉搜索树的形态为单支树，即只有左子树或者只有右子树。每次查找的搜索范围都缩小为 𝑛−1，退化为顺序查找，在最坏情况下时间复杂度为 𝑂(𝑛)。
  • 在平均情况下，二叉搜索树的平均查找长度为 𝐴𝑆𝐿=∑（本层高度*本层元素结点个数）/结点总数。所以二分搜索树的查找平均时间复杂度为 𝑂(𝑙𝑜𝑔2𝑛)。

3. 二叉搜索树的插入

二叉搜索树的插入：在二叉搜索树中插入一个值为 𝑣𝑎𝑙 的节点（假设当前二叉搜索树中不存在值为 𝑣𝑎𝑙 的节点）。

3.1 二叉搜索树的插入算法步骤

二叉搜索树的插入操作与二叉树的查找操作过程类似，具体步骤如下：

  1. 如果二叉搜索树为空，则创建一个值为 𝑣𝑎𝑙的节点，并将其作为二叉搜索树的根节点。
  2. 如果二叉搜索树不为空，则将待插入的值𝑣𝑎𝑙与二叉搜索树根节点的值𝑟𝑜𝑜𝑡.𝑣𝑎𝑙进行比较：
    1. 如果 𝑣𝑎𝑙<𝑟𝑜𝑜𝑡.𝑣𝑎𝑙，则递归将值为 𝑣𝑎𝑙 的节点插入到左子树中。
    2. 如果 𝑣𝑎𝑙>𝑟𝑜𝑜𝑡.𝑣𝑎𝑙，则递归将值为 𝑣𝑎𝑙 的节点插入到右子树中。

注意：二叉搜索树不允许存在重复节点，否则将违反其定义。因此，如果带插入节点在树中已存在，则不执行插入操作，直接返回。

3.2 二叉搜索树的插入代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}
public class Solution {  
    public TreeNode insertIntoBST(TreeNode root, int val) {  
        if (root == null) {  
            return new TreeNode(val);  
        }  
  
        if (val < root.val) {  
            root.left = insertIntoBST(root.left, val);  
        } else if (val > root.val) {  
            root.right = insertIntoBST(root.right, val);  
        }  
        // 注意这里没有处理 val == root.val 的情况，因为通常BST不允许插入重复值  
        // 如果需要插入重复值，并且保持BST的结构，可以稍微修改逻辑来处理这种情况  
  
        return root;  
    }  
}

4. 二叉搜索树的创建

二叉搜索树的创建：根据数组序列中的元素值，建立一棵二叉搜索树。

4.1 二叉搜索树的创建算法步骤

二叉搜索树的创建操作是从空树开始，按照给定数组元素的值，依次进行二叉搜索树的插入操作，最终得到一棵二叉搜索树。具体算法步骤如下：

  1. 初始化二叉搜索树为空树。
  2. 遍历数组元素，将数组元素值 𝑛𝑢𝑚𝑠[𝑖] 依次插入到二叉搜索树中。
  3. 将数组中全部元素值插入到二叉搜索树中之后，返回二叉搜索树的根节点。

4.2 二叉搜索树的创建代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}  
  
public class Solution {  
    public TreeNode insertIntoBST(TreeNode root, int val) {  
        if (root == null) {  
            return new TreeNode(val);  
        }  
  
        if (val < root.val) {  
            root.left = insertIntoBST(root.left, val);  
        } else if (val > root.val) {  
            root.right = insertIntoBST(root.right, val);  
        }  
        // 注意：这里没有处理 val == root.val 的情况  
  
        return root;  
    }  
  
    public TreeNode buildBST(int[] nums) {  
        if (nums == null || nums.length == 0) {  
            return null; // 如果数组为空，返回null  
        }  
  
        // 使用数组的第一个元素作为根节点的值  
        TreeNode root = new TreeNode(nums[0]);  
  
        // 遍历数组，将剩余元素插入BST中  
        for (int i = 1; i < nums.length; i++) {  
            insertIntoBST(root, nums[i]);  
        }  
  
        return root;  
    }  
}

5. 二叉搜索树的删除

二叉搜索树的删除：在二叉搜索树中删除值为 𝑣𝑎𝑙val 的节点。

5.1 二叉搜索树的删除算法步骤

在二叉搜索树中删除元素，首先要找到待删除节点，然后执行删除操作。根据待删除节点所在位置的不同，可以分为 33 种情况：

  1. 被删除节点的左子树为空。则令其右子树代替被删除节点的位置。
  2. 被删除节点的右子树为空。则令其左子树代替被删除节点的位置。
  3. 被删除节点的左右子树均不为空，则根据二叉搜索树的中序遍历有序性，删除该节点时，可以使用其直接前驱（或直接后继）代替被删除节点的位置。
  • 直接前驱：在中序遍历中，节点 p 的直接前驱为其左子树的最右侧的叶子节点。
  • 直接后继：在中序遍历中，节点 p 的直接后继为其右子树的最左侧的叶子节点。

二叉搜索树的删除算法步骤如下：

  1. 如果当前节点为空，则返回当前节点。
  2. 如果当前节点值大于 𝑣𝑎𝑙，则递归去左子树中搜索并删除，此时 𝑟𝑜𝑜𝑡.𝑙𝑒𝑓𝑡 也要跟着递归更新。
  3. 如果当前节点值小于 𝑣𝑎𝑙，则递归去右子树中搜索并删除，此时 𝑟𝑜𝑜𝑡.𝑟𝑖𝑔ℎ𝑡 也要跟着递归更新。
  4. 如果当前节点值等于𝑣𝑎𝑙，则该节点就是待删除节点。
    1. 如果当前节点的左子树为空，则删除该节点之后，则右子树代替当前节点位置，返回右子树。
    2. 如果当前节点的右子树为空，则删除该节点之后，则左子树代替当前节点位置，返回左子树。
    3. 如果当前节点的左右子树都有，则将左子树转移到右子树最左侧的叶子节点位置上，然后右子树代替当前节点位置。

5.2 二叉搜索树的删除代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}  
  
public class Solution {  
    public TreeNode deleteNode(TreeNode root, int key) {  
        if (root == null) {  
            return null;  
        }  
  
        if (key < root.val) {  
            root.left = deleteNode(root.left, key);  
            return root;  
        } else if (key > root.val) {  
            root.right = deleteNode(root.right, key);  
            return root;  
        }  
  
        // Node with only one child or no child  
        if (root.left == null) {  
            return root.right;  
        } else if (root.right == null) {  
            return root.left;  
        }  
  
        // Node with two children: Get the inorder successor (smallest in the right subtree)  
        TreeNode successor = root.right;  
        TreeNode successorParent = root;  
        while (successor.left != null) {  
            successorParent = successor;  
            successor = successor.left;  
        }  
  
        // If successor is not a direct child of root, remove it from its parent's left child  
        if (successorParent != root) {  
            successorParent.left = successor.right;  
        }  
  
        // Copy the inorder successor's value to this node and delete the inorder successor node  
        root.val = successor.val;  
        root.right = deleteNode(root.right, successor.val);  
  
        return root;  
    }  
}

快来参与讨论吧~

博客近期分类标签归档
项目软件开发人工智能Staller
社交友链
更多关于本站
本站由 卡卡龙 使用 Stellar 1.29.1主题创建

本站访问量 次. 本文阅读量 次.

Stellar Copyright Licenses Hexo 备案 描述文字 描述文字