树形DP知识

1. 树形动态规划简介

树形动态规划：简称为「树形 DP」，是一种在树形结构上进行推导的动态规划方法。如下图所示，树形 DP 的求解过程一般以节点从深到浅（子树从小到大）的顺序作为动态规划的「阶段」。在树形 DP 中，第 1 维通常是节点编号，代表以该节点为根的子树。

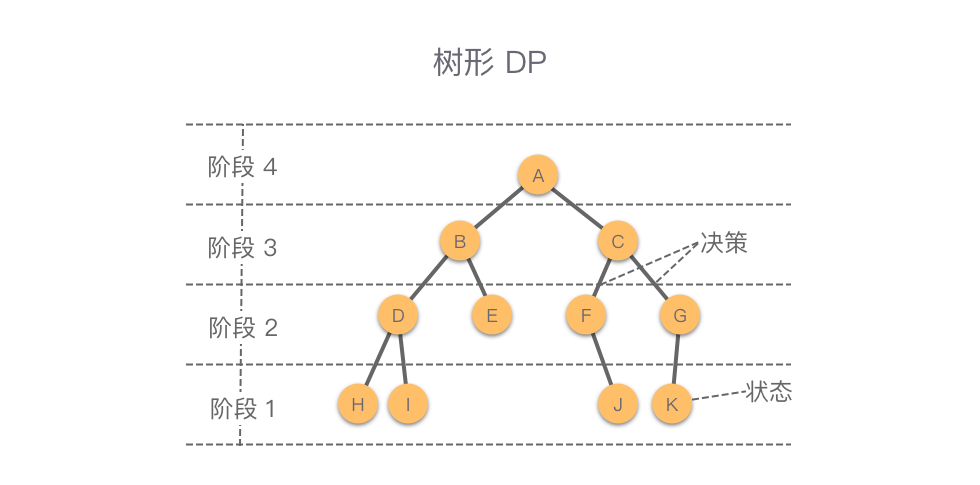
如果按照「阶段转移的方向」进行划分，可以划分为以下两种：

1. 自底向上：通过递归的方式求解每棵子树，然后在回溯时，自底向上地从子节点向上进行状态转移。只有在当前节点的所有子树求解完毕之后，才可以求解当前节点，以及继续向上进行求解。
2. 自顶向下：从根节点开始向下递归，逐层计算子节点的状态。这种方法常常使用记忆化搜索来避免重复计算，提高效率。

自顶向下的树形 DP 问题比较少见，大部分树形 DP 都是采用「自底向上」的方向进行推导。

如果按照「是否有固定根」进行划分，可以划分为以下两种：

1. 固定根的树形 DP：事先指定根节点的树形 DP 问题，通常只需要从给定的根节点开始，使用 1 次深度优先搜索。
2. 不定根的树形 DP：事先没有指定根节点的树形 DP 问题，并且根节点的变化会对一些值，例如子节点深度和、点权和等产生影响。通常需要使用 2 次深度优先搜索，第 1 次预处理诸如深度，点权和之类的信息，第 2 次开始运行换根动态规划。

2. 固定根的树形DP

2.1 固定根的树形DP基本思路

固定根的树形 DP 问题，如果是二叉树，树通常是以根节点的形式给出。我们可以直接从指定根节点出发进行深度优先搜索。如果是多叉树，树是以一张 n 个节点、n−1 条边的无向图形式给出的，并且事先给出指定根节点的编号。这种情况下，我们要先用邻接表存储下这 n 个点和 n−1 条边，然后从指定根节点出发进行深度优先搜索，并注意标记节点是否已经被访问过，以避免在遍历中沿着反向边回到父节点。

2.2 二叉树中的最大路径和

2.2.1 题目链接

• 124. 二叉树中的最大路径和 - 力扣open in new window

2.2.2 题目大意

描述：给定一个二叉树的根节点 root。

要求：返回其最大路径和。

说明：

• 路径：被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中至多出现一次。该路径至少包含一个节点，且不一定经过根节点。
• 路径和：路径中各节点值的总和。
• 树中节点数目范围是 [1,3∗10⁴]。
• −1000≤Node.val≤1000。

示例：

• 示例 1：

1
2
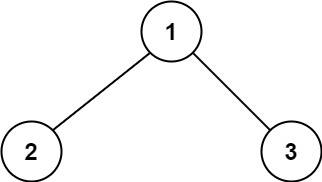
3

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

• 示例 2：

1
2
3

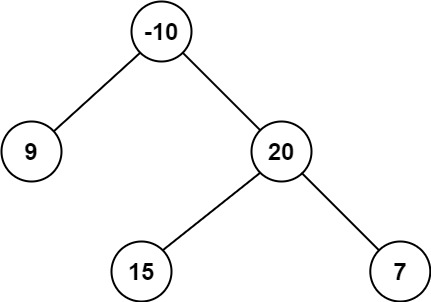
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

2.2.3 解题思路

思路 1：树形 DP + 深度优先搜索

根据最大路径和中对应路径是否穿过根节点，我们可以将二叉树分为两种：

1. 最大路径和中对应路径穿过根节点。
2. 最大路径和中对应路径不穿过根节点。

如果最大路径和中对应路径穿过根节点，则：该二叉树的最大路径和 = 左子树中最大贡献值 + 右子树中最大贡献值 + 当前节点值。

而如果最大路径和中对应路径不穿过根节点，则：该二叉树的最大路径和 = 所有子树中最大路径和。

即：**该二叉树的最大路径和 = max(左子树中最大贡献值 + 右子树中最大贡献值 + 当前节点值，所有子树中最大路径和)**。

对此我们可以使用深度优先搜索递归遍历二叉树，并在递归遍历的同时，维护一个最大路径和变量 ans。

然后定义函数 def dfs(self, node): 计算二叉树中以该节点为根节点，并且经过该节点的最大贡献值。

计算的结果可能的情况有 2 种：

1. 经过空节点的最大贡献值等于 0。
2. 经过非空节点的最大贡献值等于 当前节点值 + 左右子节点提供的最大贡献值中较大的一个。如果该贡献值为负数，可以考虑舍弃，即最大贡献值为 0。

在递归时，我们先计算左右子节点的最大贡献值，再更新维护当前最大路径和变量。最终 ans 即为答案。具体步骤如下：

1. 如果根节点 root 为空，则返回 0。
2. 递归计算左子树的最大贡献值为 leftmax。
3. 递归计算右子树的最大贡献值为 rightmax。
4. 更新维护最大路径和变量，即 self.ans=max{self.ans,leftmax+rightmax+node.val}。
5. 返回以当前节点为根节点，并且经过该节点的最大贡献值。即返回 当前节点值 + 左右子节点提供的最大贡献值中较大的一个。
6. 最终 self.ans 即为答案。

思路 1：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.ans = float('-inf')
        
    def dfs(self, node):
        if not node:
            return 0
        left_max = max(self.dfs(node.left), 0)     # 左子树提供的最大贡献值
        right_max = max(self.dfs(node.right), 0)   # 右子树提供的最大贡献值

        cur_max = left_max + right_max + node.val  # 包含当前节点和左右子树的最大路径和
        self.ans = max(self.ans, cur_max)          # 更新所有路径中的最大路径和

        return max(left_max, right_max) + node.val # 返回包含当前节点的子树的最大贡献值

    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        self.dfs(root)
        return self.ans

思路 1：复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉树的节点数目。
• 空间复杂度：O(n)。递归函数需要用到栈空间，栈空间取决于递归深度，最坏情况下递归深度为 n，所以空间复杂度为 O(n)。

2.3 相邻字符不同的最长路径

2.3.1 题目链接

• 2246. 相邻字符不同的最长路径 - 力扣open in new window

2.3.2 题目大意

描述：给定一个长度为 n 的数组 parent 来表示一棵树（即一个连通、无向、无环图）。该树的节点编号为 0∼n−1，共 n 个节点，其中根节点的编号为 0。其中 parent[i] 表示节点 i 的父节点，由于节点 0 是根节点，所以 parent[0]==−1。再给定一个长度为 n 的字符串，其中 s[i] 表示分配给节点 i 的字符。

要求：找出路径上任意一对相邻节点都没有分配到相同字符的最长路径，并返回该路径的长度。

说明：

• n==parent.length==s.length。
• 1≤n≤10⁵。
• 对所有 i≥1，0≤parent[i]≤n−1 均成立。
• parent[0]==−1。
• parent 表示一棵有效的树。
• s 仅由小写英文字母组成。

示例：

• 示例 1：

1
2
3
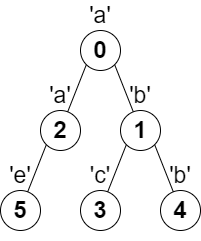
4

输入：parent = [-1,0,0,1,1,2], s = "abacbe"
输出：3
解释：任意一对相邻节点字符都不同的最长路径是：0 -> 1 -> 3 。该路径的长度是 3 ，所以返回 3。
可以证明不存在满足上述条件且比 3 更长的路径。

• 示例 2：

1
2
3

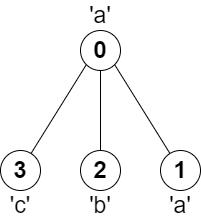
输入：parent = [-1,0,0,0], s = "aabc"
输出：3
解释：任意一对相邻节点字符都不同的最长路径是：2 -> 0 -> 3 。该路径的长度为 3 ，所以返回 3。

2.3.3 解题思路

思路 1：树形 DP + 深度优先搜索

因为题目给定的是表示父子节点的 parent 数组，为了方便递归遍历相邻节点，我们可以根据 partent数组，建立一个由父节点指向子节点的有向图 graph。

如果不考虑相邻节点是否为相同字符这一条件，那么这道题就是在求树的直径（树的最长路径长度）中的节点个数。

对于根节点为 u 的树来说：

1. 如果其最长路径经过根节点 u，则：最长路径长度 = 某子树中的最长路径长度 + 另一子树中的最长路径长度 + 1。
2. 如果其最长路径不经过根节点 u，则：最长路径长度 = 某个子树中的最长路径长度。

即：**最长路径长度 = max(某子树中的最长路径长度 + 另一子树中的最长路径长度 + 1，某个子树中的最长路径长度)**。

对此，我们可以使用深度优先搜索递归遍历 u 的所有相邻节点 v，并在递归遍历的同时，维护一个全局最大路径和变量 ans，以及当前节点 u 的最大路径长度变量 ulen。

1. 先计算出从相邻节点 v 出发的最长路径长度 vlen。
2. 更新维护全局最长路径长度为 self.ans=max(self.ans,ulen+vlen+1)。
3. 更新维护当前节点 u 的最长路径长度为 ulen=max(ulen,vlen+1)。

因为题目限定了「相邻节点字符不同」，所以在更新全局最长路径长度和当前节点 u 的最长路径长度时，我们需要判断一下节点 u 与相邻节点 v 的字符是否相同，只有在字符不同的条件下，才能够更新维护。

最后，因为题目要求的是树的直径（树的最长路径长度）中的节点个数，而：路径的节点 = 路径长度 + 1，所以最后我们返回 self.ans+1 作为答案。

思路 1：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution:
    def longestPath(self, parent: List[int], s: str) -> int:
        size = len(parent)

        # 根据 parent 数组，建立有向图
        graph = [[] for _ in range(size)]
        for i in range(1, size):
            graph[parent[i]].append(i)

        ans = 0
        def dfs(u):
            nonlocal ans
            u_len = 0                                   # u 节点的最大路径长度
            for v in graph[u]:                          # 遍历 u 节点的相邻节点
                v_len = dfs(v)                          # 相邻节点的最大路径长度
                if s[u] != s[v]:                        # 相邻节点字符不同
                    ans = max(ans, u_len + v_len + 1)   # 维护最大路径长度
                    u_len = max(u_len, v_len + 1)       # 更新 u 节点的最大路径长度
            return u_len                                # 返回 u 节点的最大路径长度

        dfs(0)
        return ans + 1

思路 1：复杂度分析

• 时间复杂度：O(n)，其中 n 是树的节点数目。
• 空间复杂度：O(n)。

3. 不定根的树形 DP

3.1 不定根的树形 DP 基本思路

不定根的树形 DP 问题，如果是二叉树，树通常是以一张 n 个节点、n−1条边的无向图形式给出的，并且事先没有指定根节点。通常需要以「每个节点为根节点」进行一系列统计。

这种情况下，我们一般通过「两次扫描与换根法」的方法求解这类题目：

1. 第一次扫描时，任选一个节点为根，在「有固定根的树」上执行一次树形 DP，预处理树的一些相关信息。
2. 第二次扫描时，从刚才的根节点出发，对整棵树再执行一次深度优先搜索，同时携带根节点的一些信息提供给子节点进行推导，计算出「换根」之后的解。

3.2 最小高度树

3.2.1 题目链接

• 310. 最小高度树 - 力扣open in new window

3.2.2 题目大意

描述：有一棵包含 n 个节点的树，节点编号为 0∼n−1。给定一个数字 n 和一个有 n−1 条无向边的 edges 列表来表示这棵树。其中 edges[i]=[ai,bi] 表示树中节点 ai 和 bi之间存在一条无向边。

可以选择树中的任何一个节点作为根，当选择节点 x 作为根节点时，设结果树的高度为 h。在所有可能的树种，具有最小高度的树（即 min(h)）被成为最小高度树。

要求：找到所有的最小高度树并按照任意顺序返回他们的根节点编号列表。

说明：

• 树的高度：指根节点和叶子节点之间最长向下路径上边的数量。
• 1≤n≤2×10⁴。
• edges.length==n−1。
• 0≤ai,bi<n。
• ai≠bi。
• 所有 (ai,bi) 互不相同。
• 给定的输入保证是一棵树，并且不会有重复的边。

示例：

• 示例 1：

1
2
3

输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

• 示例 2：

1
2

输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

3.2.3 解题思路

思路 1：树形 DP + 二次遍历换根法

最容易想到的做法是：枚举 n 个节点，以每个节点为根节点，然后进行深度优先搜索，求出每棵树的高度。最后求出所有树中的最小高度即为答案。但这种做法的时间复杂度为 O(n²)，而 n 的范围为 [1,2×10⁴]，这样做会导致超时，因此需要进行优化。

在上面的算法中，在一轮深度优先搜索中，除了可以得到整棵树的高度之外，在搜索过程中，其实还能得到以每个子节点为根节点的树的高度。如果我们能够利用这些子树的高度信息，快速得到以其他节点为根节点的树的高度，那么我们就能改进算法，以更小的时间复杂度解决这道题。这就是二次遍历与换根法的思想。

1. 第一次遍历：自底向上的计算出每个节点 u 向下走（即由父节点 u 向子节点 v 走）的最长路径 down1[u]、次长路径 down2[i]，并记录向下走最长路径所经过的子节点 p[u]，方便第二次遍历时计算。
2. 第二次遍历：自顶向下的计算出每个节点v向上走（即由子节点v向父节点u走）的最长路径up[v]。需要注意判断u向下走的最长路径是否经过了节点v。
   1. 如果经过了节点 v，则向上走的最长路径，取决于「父节点 u 向上走的最长路径」与「父节点 u 向下走的次长路径」 的较大值，再加上 1。
   2. 如果没有经过节点 v，则向上走的最长路径，取决于「父节点 u 向上走的最长路径」与「父节点 u 向下走的最长路径」 的较大值，再加上 1。
3. 接下来，我们通过枚举 n 个节点向上走的最长路径与向下走的最长路径，从而找出所有树中的最小高度，并将所有最小高度树的根节点放入答案数组中并返回。

整个算法具体步骤如下：

1. 使用邻接表的形式存储树。
2. 定义第一个递归函数dfs(u, fa)用于计算每个节点向下走的最长路径down1[u]、次长路径down2[u]，并记录向下走的最长路径所经过的子节点p[u]。
   1. 对当前节点的相邻节点进行遍历。
   2. 如果相邻节点是父节点，则跳过。
   3. 递归调用 dfs(v, u) 函数计算邻居节点的信息。
   4. 根据邻居节点的信息计算当前节点的高度，并更新当前节点向下走的最长路径 down1[u]、当前节点向下走的次长路径 down2、取得最长路径的子节点 p[u]。
3. 定义第二个递归函数reroot(u, fa)用于计算每个节点作为新的根节点时向上走的最长路径up[v]。
   1. 对当前节点的相邻节点进行遍历。
   2. 如果相邻节点是父节点，则跳过。
   3. 根据当前节点u的高度和相邻节点v的信息更新up[v]。同时需要判断节点u向下走的最长路径是否经过了节点v。
      1. 如果经过了节点 v，则向上走的最长路径，取决于「父节点 u 向上走的最长路径」与「父节点 u 向下走的次长路径」 的较大值，再加上 1，即：up[v]=max(up[u],down2[u])+1。
      2. 如果没有经过节点 v，则向上走的最长路径，取决于「父节点 u 向上走的最长路径」与「父节点 u* 向下走的最长路径」 的较大值，再加上 1，即：up[v]=max(up[u],down1[u])+1。
   4. 递归调用 reroot(v, u) 函数计算邻居节点的信息。
4. 调用 dfs(0, -1) 函数计算每个节点的最长路径。
5. 调用 reroot(0, -1) 函数计算每个节点作为新的根节点时的最长路径。
6. 找到所有树中的最小高度。
7. 将所有最小高度的节点放入答案数组中并返回。

思路 1：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        graph = [[] for _ in range(n)]
        for u, v in edges:
            graph[u].append(v)
            graph[v].append(u)
		
        # down1 用于记录向下走的最长路径 
        down1 = [0 for _ in range(n)]
        # down2 用于记录向下走的最长路径
        down2 = [0 for _ in range(n)]
        p = [0 for _ in range(n)]
        # 自底向上记录最长路径、次长路径
        def dfs(u, fa):
            for v in graph[u]:
                if v == fa:
                    continue
                # 自底向上统计信息
                dfs(v, u)                   
                height = down1[v] + 1
                if height >= down1[u]:
                    down2[u] = down1[u]
                    down1[u] = height
                    p[u] = v
                elif height > down2[u]:
                    down2[u] = height

        # 进行换根动态规划，自顶向下统计向上走的最长路径
        up = [0 for _ in range(n)]
        def reroot(u, fa):
            for v in graph[u]:
                if v == fa:
                    continue
                if p[u] == v:
                    up[v] = max(up[u], down2[u]) + 1
                else:
                    up[v] = max(up[u], down1[u]) + 1
                # 自顶向下统计信息
                reroot(v, u)                            

        dfs(0, -1)
        reroot(0, -1)

        # 找到所有树中的最小高度
        min_h = 1e9
        for i in range(n):
            min_h = min(min_h, max(down1[i], up[i]))

        # 将所有最小高度的节点放入答案数组中并返回
        res = []
        for i in range(n):
            if max(down1[i], up[i]) == min_h:
                res.append(i)

        return res

思路 1：复杂度分析

• 时间复杂度：O(n)。
• 空间复杂度：O(n)。