背包问题<二>

3. 完全背包问题

完全背包问题：有 n 种物品和一个最多能装重量为 W 的背包，第 i 种物品的重量为 weight[i]，价值为 value[i]，每种物品数量没有限制。请问在总重量不超过背包载重上限的情况下，能装入背包的最大价值是多少？

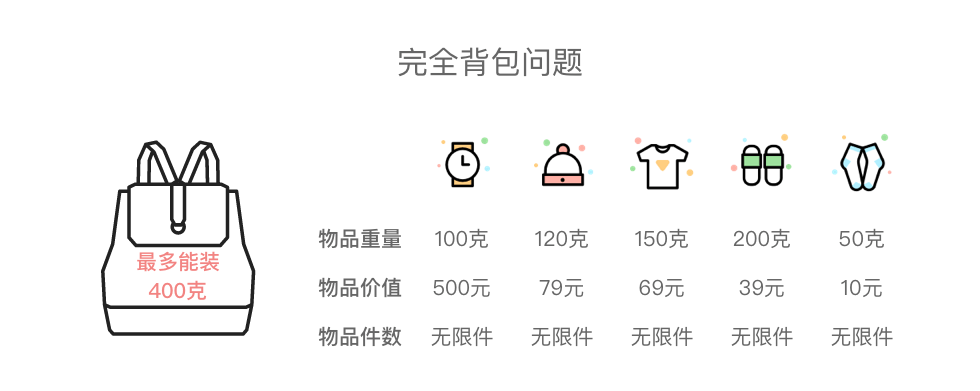
3.1 完全背包问题基本思路

完全背包问题的特点：每种物品有无限件。

思路 1：动态规划 + 二维基本思路

1.划分阶段

按照物品种类的序号、当前背包的载重上限进行阶段划分。

2.定义状态

定义状态 dp[i] [w] 表示为：前 i 种物品放入一个最多能装重量为 w 的背包中，可以获得的最大价值。

状态 dp[i] [w] 是一个二维数组，其中第一维代表「当前正在考虑的物品种类」，第二维表示「当前背包的载重上限」，二维数组值表示「可以获得的最大价值」。

3.状态转移方程

由于每种物品可选的数量没有限制，因此状态 dp[i] [w]可能从以下方案中选择最大值：

1. 选择 0 件第 i−1 件物品：可以获得的最大价值为 dp[i−1] [w]
2. 选择 1 件第 i−1 件物品：可以获得的最大价值为 dp[i−1] [w−weight[i−1]]+value[i−1]。
3. 选择 2 件第 i−1 件物品：可以获得的最大价值为 dp[i−1] [w−2×weight[i−1]]+2×value[i−1]。
4. ……
5. 选择 k 件第 i−1 件物品：可以获得的最大价值为 dp[i−1] [w−k×weight[i−1]]+k×value[i−1]。

注意：选择 k 件第 i−1 件物品的条件是 0≤k×weight[i−1]≤w。

则状态转移方程为：

4.初始条件

• 如果背包载重上限为 0，则无论选取什么物品，可以获得的最大价值一定是 0，即 dp[i] [0]=0,0≤i≤size。
• 无论背包载重上限是多少，前 0 种物品所能获得的最大价值一定为 0，即 dp[0] [w]=0,0≤w≤W。

5.最终结果

根据我们之前定义的状态，dp[i] [w] 表示为：前 i 种物品放入一个最多能装重量为 w 的背包中，可以获得的最大价值。则最终结果为 dp[size] [W]，其中 size 为物品的种类数，W 为背包的载重上限。

思路 1：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

public int completePackMethod1(int[] weight, int[] value, int W) {
        int size = weight.length;
        int[][] dp = new int[size + 1][W + 1];

        // 枚举前 i 种物品
        for (int i = 1; i <= size; i++) {
            // 枚举背包装载重量
            for (int w = 0; w <= W; w++) {
                // 枚举第 i - 1 种物品能取个数
                for (int k = 0; k <= w / weight[i - 1]; k++) {
                    // dp[i][w] 取所有 dp[i - 1][w - k * weight[i - 1] + k * value[i - 1] 中最大值
                    dp[i][w] = Math.max(dp[i][w], dp[i - 1][w - k * weight[i - 1]] + k * value[i - 1]);
                }
            }
        }

        return dp[size][W];
}

思路 1：复杂度分析

3.2 完全背包问题状态转移方程优化

上之前的思路中，对于每种物品而言，每次我们都需要枚举所有可行的物品数目 k，这就大大增加了时间复杂度。

实际上，我们可以对之前的状态转移方程进行一些优化，从而减少一下算法的时间复杂度。

我们将之前的状态转移方程

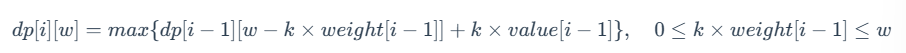
进行展开：

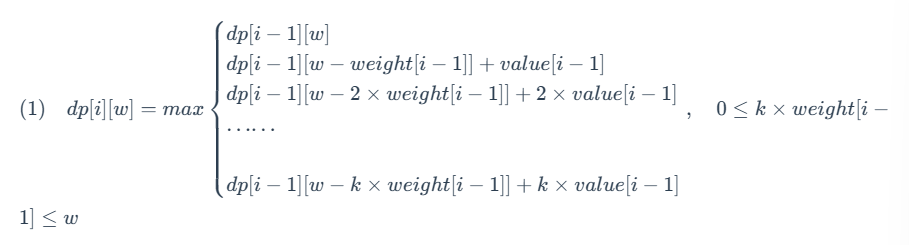
而对于 dp[i] [w−weight[i−1]] 我们有：

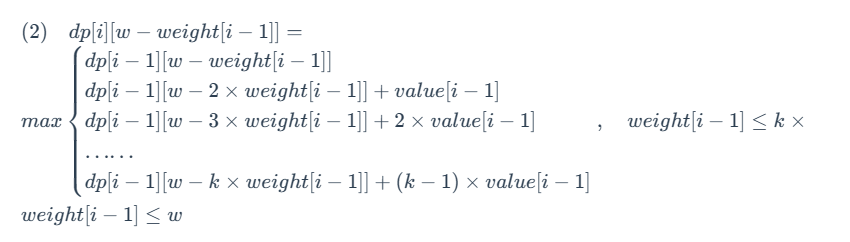
通过观察可以发现：

1. (1) 式中共有 k+1 项，(2) 式中共有 k 项；
2. (2) 式整个式子与 (1) 式第 1∼k+1 项刚好相差一个 value[i−1]。

则我们将 (2) 式加上 value[i−1]，再代入 (1) 式中，可得到简化后的「状态转移方程」为：

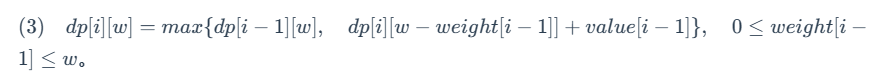
简化后的「状态转移方程」去除了对物品件数的依赖，也就不需要遍历 k 了，三层循环降为了两层循环。

注意：式 (3) 的满足条件为 0≤weight[i−1]≤w。当 w<weight[i−1] 时，dp[i] [w]=dp[i−1] [w]。

则状态转移方程为：

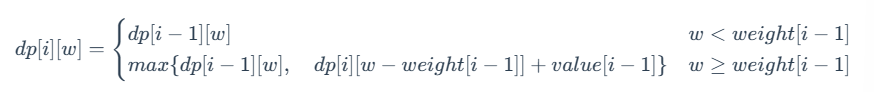
从上述状态转移方程我们可以看出：该式子与 0-1 背包问题中「思路 1」的状态转移式极其相似。

唯一区别点在于：

1. 0-1 背包问题中状态为 dp[i−1] [w−weight[i−1]]+value[i−1]，这是第* i−1* 阶段上的状态值。
2. 完全背包问题中状态为 dp[i] [w−weight[i−1]]+value[i−1]，这是第 i 阶段上的状态值。

思路 2：动态规划 + 状态转移方程优化

1.划分阶段

按照物品种类的序号、当前背包的载重上限进行阶段划分。

2.定义状态

定义状态 dp[i] [w] 表示为：前 i 种物品放入一个最多能装重量为 w 的背包中，可以获得的最大价值。

状态 dp[i] [w]是一个二维数组，其中第一维代表「当前正在考虑的物品种类」，第二维表示「当前背包的载重上限」，二维数组值表示「可以获得的最大价值」。

3.状态转移方程

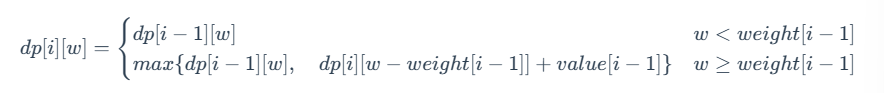
4.初始条件

• 如果背包载重上限为 0，则无论选取什么物品，可以获得的最大价值一定是 0，即 dp[i] [0]=0,0≤i≤size。
• 无论背包载重上限是多少，前 0 种物品所能获得的最大价值一定为 0，即 dp[0] [w]=0,0≤w≤W。

5.最终结果

根据我们之前定义的状态，dp[i] [w] 表示为：前 i 种物品放入一个最多能装重量为 w 的背包中，可以获得的最大价值。则最终结果为 dp[size] [W]，其中 size为物品的种类数，W 为背包的载重上限。

思路 2：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

public int completePackMethod2(int[] weight, int[] value, int W) {
        int size = weight.length;
        int[][] dp = new int[size + 1][W + 1];

        // 枚举前 i 种物品
        for (int i = 1; i <= size; i++) {
            // 枚举背包装载重量
            for (int w = 0; w <= W; w++) {
                // 第 i - 1 件物品装不下
                if (w < weight[i - 1]) {
                    // dp[i][w] 取「前 i - 1 种物品装入载重为 w 的背包中的最大价值」
                    dp[i][w] = dp[i - 1][w];
                } else {
                    // dp[i][w] 取「前 i - 1 种物品装入载重为 w 的背包中的最大价值」与「前 i 种物品装入载重为 w - weight[i - 1] 的背包中，再装入 1 件第 i - 1 种物品所得的最大价值」两者中的最大值
                    dp[i][w] = Math.max(dp[i - 1][w], dp[i][w - weight[i - 1]] + value[i - 1]);
                }
            }
        }

        return dp[size][W];
}

思路 2：复杂度分析

• 时间复杂度：O(n×W)，其中 n 为物品种类数量，W 为背包的载重上限。
• 空间复杂度：O(n×W)。

3.3 完全背包问题滚动数组优化

通过观察「思路 2」中的状态转移方程

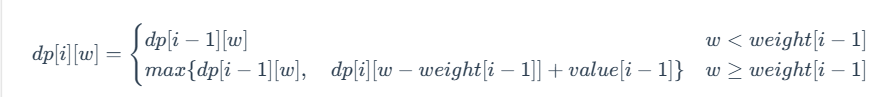
可以看出：我们只用到了当前行（第 i 行）的 dp[i] [w]、dp[i] [w−weight[i−1]]，以及上一行（第 i−1 行）的 dp[i−1] [w]。

所以我们没必要保存所有阶段的状态，只需要使用一个一维数组 dp[w] 保存上一阶段的所有状态，采用使用「滚动数组」的方式对空间进行优化（去掉动态规划状态的第一维）。

思路 3：动态规划 + 滚动数组优化

1.划分阶段

按照当前背包的载重上限进行阶段划分。

2.定义状态

定义状态 dp[w] 表示为：将物品装入最多能装重量为 w 的背包中，可以获得的最大价值。

3.状态转移方程

注意：这里的 dp[w−weight[i−1]]是第 i 轮计算之后的「第 i 阶段的状态值」。

因为在计算 dp[w]时，我们需要用到第 i 轮计算之后的 dp[w−weight[i−1]]，所以我们需要按照「从 0∼W 正序递推的方式」递推 dp[w]，这样才能得到正确的结果。

因为 w<weight[i−1] 时，dp[w] 只能取上一阶段的 dp[w]，其值相当于没有变化，这部分可以不做处理。所以我们在正序递推 dp[w] 时，只需从 weight[i−1] 开始遍历即可。

4.初始条件

• 无论背包载重上限为多少，只要不选择物品，可以获得的最大价值一定是 0，即 dp[w]=0,0≤w≤W。

5.最终结果

根据我们之前定义的状态， dp[w] 表示为：将物品装入最多能装重量为 w 的背包中，可以获得的最大价值。则最终结果为 dp[W]，其中 W 为背包的载重上限。

思路 3：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

public int completePackMethod3(int[] weight, int[] value, int W) {
        int size = weight.length;
        int[] dp = new int[W + 1];

        // 枚举前 i 种物品
        for (int i = 1; i <= size; i++) {
            // 正序枚举背包装载重量
            for (int w = weight[i - 1]; w <= W; w++) {
                // dp[w] 取「前 i - 1 种物品装入载重为 w 的背包中的最大价值」与「前 i 种物品装入载重为 w - weight[i - 1] 的背包中，再装入 1 件第 i - 1 种物品所得的最大价值」两者中的最大值
                dp[w] = Math.max(dp[w], dp[w - weight[i - 1]] + value[i - 1]);
            }
        }

        return dp[W];
}

通过观察「0-1 背包问题滚动数组优化的代码」和「完全背包问题滚动数组优化的代码」可以看出，两者的唯一区别在于：

1. 0-1 背包问题滚动数组优化的代码采用了「从 W∼weight[i−1]逆序递推的方式」。
2. 完全背包问题滚动数组优化的代码采用了「从 weight[i−1]∼W正序递推的方式」。

思路 3：复杂度分析

• 时间复杂度：O(n×W)，其中 n 为物品种类数量，W 为背包的载重上限。
• 空间复杂度：O(W)。