算法：区间DP基础知识

1. 区间动态规划简介

1.1 区间动态规划定义

区间动态规划：线性 DP 的一种，简称为「区间 DP」。以「区间长度」划分阶段，以两个坐标（区间的左、右端点）作为状态的维度。一个状态通常由被它包含且比它更小的区间状态转移而来。

区间 DP 的主要思想就是：先在小区间内得到最优解，再利用小区间的最优解合并，从而得到大区间的最优解，最终得到整个区间的最优解。

根据小区间向大区间转移情况的不同，常见的区间 DP 问题可以分为两种：

单个区间从中间向两侧更大区间转移的区间 DP 问题。比如从区间 [i+1,j−1] 转移到更大区间 [i,j]。
多个（大于等于 2 个）小区间转移到大区间的区间 DP 问题。比如从区间 [i,k]和区间 [k,j] 转移到区间 [i,j]。

下面我们讲解一下这两种区间 DP 问题的基本解题思路。

1.2 区间 DP 问题的基本思路

1.2.1 第 1 种区间 DP 问题基本思路

从中间向两侧转移的区间 DP 问题的状态转移方程一般为：dp[i] [j]=max{dp[i+1] [j−1],dp[i+1] [j],dp[i] [j−1]}+cost[i] [j],i≤j。

其中 dp[i] [j] 表示为：区间 [i,j]（即下标位置 i 到下标位置 j 上所有元素）上的最大价值。
cost 表示为：从小区间转移到区间 [i,j] 的代价。
这里的 max/min 取决于题目是求最大值还是求最小值。

从中间向两侧转移的区间 DP 问题的基本解题思路如下：

枚举区间的起点；
枚举区间的终点；
根据状态转移方程计算从小区间转移到更大区间后的最优值。

对应代码如下：

for i in range(size - 1, -1, -1):       # 枚举区间起点
    for j in range(i + 1, size):        # 枚举区间终点
        # 状态转移方程，计算转移到更大区间后的最优值
        dp[i][j] = max(dp[i + 1][j - 1], dp[i + 1][j], dp[i][j - 1]) + cost[i][j]

1.2.3 第 2 种区间 DP 问题基本思路

多个（大于等于 2 个）小区间转移到大区间的区间 DP 问题的状态转移方程一般为：dp[i] [j]=max/min{dp[i] [k]+dp[k+1] [j]+cost[i] [j]},i<k≤j。

其中状态 dp[i] [j]表示为：区间 [i,j] （即下标位置 i 到下标位置 j 上所有元素）上的最大价值。
cost[i] [j] 表示为：将两个区间 [i,k]与 [k+1,j] 中的元素合并为区间 [i,j] 中的元素的代价。
这里的 max/min 取决于题目是求最大值还是求最小值。

多个小区间转移到大区间的区间 DP 问题的基本解题思路如下：

枚举区间长度；
枚举区间的起点，根据区间起点和区间长度得出区间终点；
枚举区间的分割点，根据状态转移方程计算合并区间后的最优值。

对应代码如下：

for l in range(1, n):               # 枚举区间长度
    for i in range(n):              # 枚举区间起点
        j = i + l - 1               # 根据起点和长度得到终点
        if j >= n:
            break
        dp[i][j] = float('-inf')    # 初始化 dp[i][j]
        for k in range(i, j + 1):   # 枚举区间分割点
            # 状态转移方程，计算合并区间后的最优值
            dp[i][j] = max(dp[i][j], dp[i][k] + dp[k + 1][j] + cost[i][j])

2. 区间 DP 问题的应用

下面我们根据几个例子来讲解一下区间 DP 问题的具体解题思路。

2.1 最长回文子序列

2.1.1 题目链接

516. 最长回文子序列 - 力扣open in new window

2.1.2 题目大意

描述：给定一个字符串 s。

要求：找出其中最长的回文子序列，并返回该序列的长度。

说明：

子序列：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。
1≤s.length≤1000。
s 仅由小写英文字母组成。

示例：

示例 1：

1
2
3

输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb"。

示例 2：

1
2
3

输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb"。

2.1.3 解题思路

思路 1：动态规划

1. 划分阶段

按照区间长度进行阶段划分。

2. 定义状态

定义状态 dp[i] [j] 表示为：字符串 s 在区间 [i,j] 范围内的最长回文子序列长度。

3. 状态转移方程

4. 初始条件

单个字符的最长回文序列是 1，即 dp[i] [i]=1。

5. 最终结果

思路 1：代码

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        size = len(s)
        dp = [[0 for _ in range(size)] for _ in range(size)]
        for i in range(size):
            dp[i][i] = 1

        for i in range(size - 1, -1, -1):
            for j in range(i + 1, size):
                if s[i] == s[j]:
                    dp[i][j] = dp[i + 1][j - 1] + 2
                else:
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])

        return dp[0][size - 1]

思路 1：复杂度分析

时间复杂度：O(n²)，其中 n 为字符串 s 的长度。
空间复杂度：O(n²)。

2.2 戳气球

2.2.1 题目链接

312. 戳气球 - 力扣open in new window

2.2.2 题目大意

描述：有 n 个气球，编号为 0∼n−1，每个气球上都有一个数字，这些数字存在数组 nums 中。现在开始戳破气球。其中戳破第 i 个气球，可以获得 nums[i−1]×nums[i]×nums[i+1]枚硬币，这里的 i−1 和 i+1 代表和 i 相邻的两个气球的编号。如果 i−1 或 i+1 超出了数组的边界，那么就当它是一个数字为 1 的气球。

要求：求出能获得硬币的最大数量。

说明：

n==nums.length。
1≤n≤300。
0≤nums[i]≤100。

示例：

示例 1：

输入：nums = [3,1,5,8]
输出：167
解释：
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins =  3*1*5    +   3*5*8   +  1*3*8  + 1*8*1 = 167

示例 2：

输入：nums = [1,5]
输出：10
解释：
nums = [1,5] --> [5] --> []
coins = 1*1*5 +  1*5*1 = 10

2.2.3 解题思路

思路 1：动态规划

根据题意，如果 i−1 或 i+1 超出了数组的边界，那么就当它是一个数字为 1 的气球。我们可以预先在 nums 的首尾位置，添加两个数字为 1 的虚拟气球，这样变成了 n+2 个气球，气球对应编号也变为了 0∼n+1。

对应问题也变成了：给定 n+2个气球，每个气球上有 1 个数字，代表气球上的硬币数量，当我们戳破气球 nums[i] 时，就能得到对应 nums[i−1]×nums[i]×nums[i+1] 枚硬币。现在要戳破 0∼n+1 之间的所有气球（不包括编号 0 和编号 n+1 的气球），请问最多能获得多少枚硬币？

1. 划分阶段

按照区间长度进行阶段划分。

2. 定义状态

定义状态 dp[i] [j]表示为：戳破所有气球 i 与气球 j 之间的气球（不包含气球 i 和气球 j），所能获取的最多硬币数。

3. 状态转移方程

假设气球 i 与气球 j 之间最后一个被戳破的气球编号为 k。则 dp[i] [j] 取决于由 k 作为分割点分割出的两个区间 (i,k) 与

(k,j) 上所能获取的最多硬币数 + 戳破气球 k 所能获得的硬币数，即状态转移方程为：

dp[i] [j]=max{dp[i] [k]+dp[k] [j]+nums[i]×nums[k]×nums[j]},i<k<j

4. 初始条件

dp[i] [j] 表示的是开区间，则 i<j−1。而当 i≥j−1 时，所能获得的硬币数为 0，即 dp[i] [j]=0,i≥j−1。

5. 最终结果

根据我们之前定义的状态，dp[i] [j] 表示为：戳破所有气球 i 与气球 j 之间的气球（不包含气球 i 和气球 j），所能获取的最多硬币数。所以最终结果为 dp[0] [n+1]。

思路 1：代码

class Solution:
    def maxCoins(self, nums: List[int]) -> int:
        size = len(nums)
        arr = [0 for _ in range(size + 2)]
        arr[0] = arr[size + 1] = 1
        for i in range(1, size + 1):
            arr[i] = nums[i - 1]
        
        dp = [[0 for _ in range(size + 2)] for _ in range(size + 2)]

        for l in range(3, size + 3):
            for i in range(0, size + 2):
                j = i + l - 1
                if j >= size + 2:
                    break
                for k in range(i + 1, j):
                    dp[i][j] = max(dp[i][j], dp[i][k] + dp[k][j] + arr[i] * arr[j] * arr[k])
        
        return dp[0][size + 1]

思路 1：复杂度分析

时间复杂度：O(n³)，其中 n 为气球数量。
空间复杂度：O(n²)。

2.3 切棍子的最小成本

2.3.1 题目链接

1547. 切棍子的最小成本 - 力扣open in new window

2.3.2 题目大意

描述：给定一个整数 n，代表一根长度为 n 个单位的木根，木棍从 0∼n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

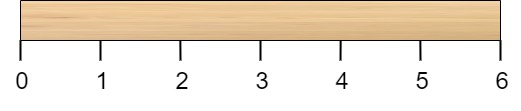
再给定一个整数数组 cuts，其中 cuts[i] 表示需要将棍子切开的位置。

我们可以按照顺序完成切割，也可以根据需要更改切割顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是所有次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根小木棍的长度和就是切割前木棍的长度）。

要求：返回切棍子的最小总成本。

说明：

2≤n≤10⁶。
1≤cuts.length≤min(n−1,100)。
1≤cuts[i]≤n−1。
cuts 数组中的所有整数都互不相同。

示例：

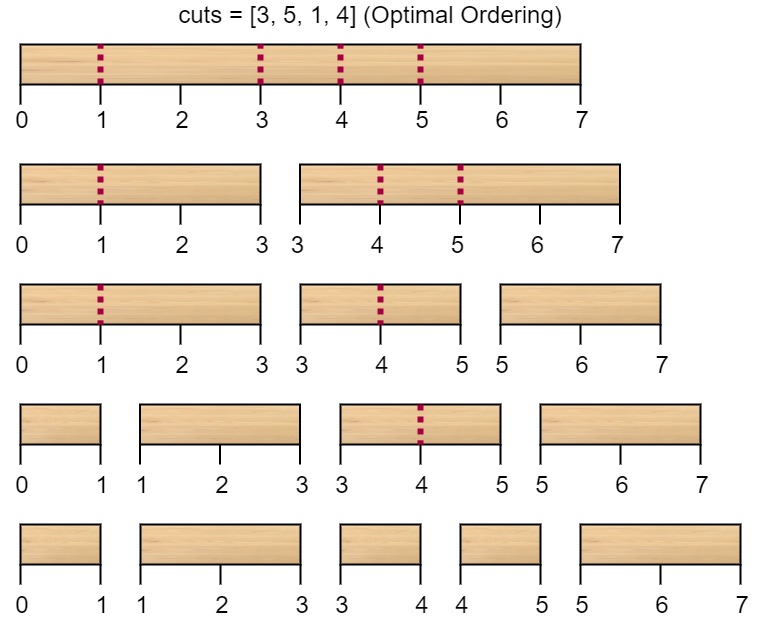
示例 1：

输入：n = 7, cuts = [1,3,4,5]
输出：16
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示。
第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

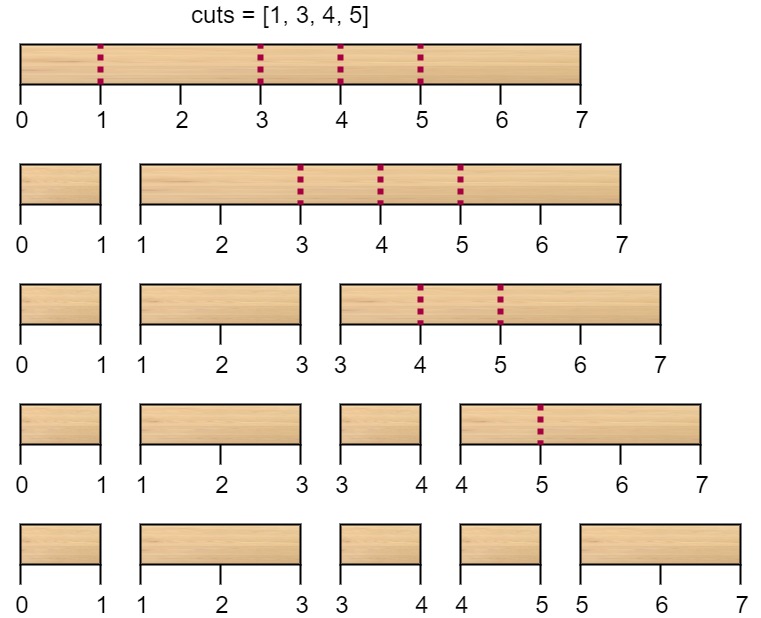
示例 2：

1
2
3

输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。

2.3.3 解题思路

思路 1：动态规划

我们可以预先在数组 cuts 种添加位置 0 和位置 n，然后对数组 cuts进行排序。这样待切割的木棍就对应了数组中连续元素构成的「区间」。

1. 划分阶段

按照区间长度进行阶段划分。

2. 定义状态

定义状态 dp[i] [j] 表示为：切割区间为 [i,j] 上的小木棍的最小成本。

3. 状态转移方程

假设位置 i 与位置 j 之间最后一个切割的位置为 k，则 dp[i] [j]取决与由 k 作为切割点分割出的两个区间 [i,k] 与 [k,j] 上的最小成本 + 切割位置 k 所带来的成本。

而切割位置 k 所带来的成本是这段区间所代表的小木棍的长度，即 cuts[j]−cuts[i]。

则状态转移方程为：dp[i] [j] = min{dp[i] [k]+dp[k] [j]+cuts[j]−cuts[i]},i<k<j

4. 初始条件

相邻位置之间没有切割点，不需要切割，最小成本为 0，即 dp[i−1] [i]=0。
其余位置默认为最小成本为一个极大值，即 dp[i] [j]=∞,i+1≠j。

5. 最终结果

根据我们之前定义的状态，dp[i] [j] 表示为：切割区间为 [i,j] 上的小木棍的最小成本。所以最终结果为 dp[0] [size−1]。

思路 1：代码

class Solution:
    def minCost(self, n: int, cuts: List[int]) -> int:
        cuts.append(0)
        cuts.append(n)
        cuts.sort()
        
        size = len(cuts)
        dp = [[float('inf') for _ in range(size)] for _ in range(size)]
        for i in range(1, size):
            dp[i - 1][i] = 0

        for l in range(3, size + 1):        # 枚举区间长度
            for i in range(size):           # 枚举区间起点
                j = i + l - 1               # 根据起点和长度得到终点                            
                if j >= size:      
                    continue
                dp[i][j] = float('inf')
                for k in range(i + 1, j):   # 枚举区间分割点
                    # 状态转移方程，计算合并区间后的最优值
                    dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + cuts[j] - cuts[i])
        return dp[0][size - 1]

思路 1：复杂度分析

时间复杂度：O(m³)，其中 m 为数组 cuts 的元素个数。
空间复杂度：O(m²)。