6. 分组背包问题

分组背包问题：有 n 组物品和一个最多能装重量为 W 的背包，第 i 组物品的件数为 groupcount[i]，第 i 组的第 j 个物品重量为 weight[i] [j]，价值为 value[i] [j]。每组物品中最多只能选择 1 件物品装入背包。请问在总重量不超过背包载重上限的情况下，能装入背包的最大价值是多少？

img

6.1 分组背包问题基本思路

思路 1：动态规划 + 二维基本思路

  1. 划分阶段

按照物品种类的序号、当前背包的载重上限进行阶段划分。

  1. 定义状态

定义状态 dp[i] [w] 表示为：前 i 组物品放入一个最多能装重量为 w 的背包中，可以获得的最大价值。

状态 dp[i] [w] 是一个二维数组，其中第一维代表「当前正在考虑的物品组数」，第二维表示「当前背包的载重上限」，二维数组值表示「可以获得的最大价值」。

  1. 状态转移方程

image-20240323121014196

  1. 初始条件
  • 如果背包载重上限为 0，则无论选取什么物品，可以获得的最大价值一定是 0，即 dp[i] [0]=0,0≤i≤size。
  • 无论背包载重上限是多少，前 0 组物品所能获得的最大价值一定为 0，即 dp[0] [w]=0,0≤w≤W。
  1. 最终结果

根据我们之前定义的状态，dp[i] [w] 表示为：前 i 组物品放入一个最多能装重量为 w 的背包中，可以获得的最大价值。则最终结果为 dp[size] [W]，其中 size 为物品的种类数W 为背包的载重上限。

思路 1：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    # 思路 1：动态规划 + 二维基本思路
    def groupPackMethod1(self, group_count: [int], weight: [[int]], value: [[int]], W: int):
        size = len(group_count)
        dp = [[0 for _ in range(W + 1)] for _ in range(size + 1)]
        
        # 枚举前 i 组物品
        for i in range(1, size + 1):
            # 枚举背包装载重量
            for w in range(W + 1):
                # 枚举第 i - 1 组物品能取个数
                dp[i][w] = dp[i - 1][w]
                for k in range(group_count[i - 1]):
                    if w >= weight[i - 1][k]:
                        # dp[i][w] 取所有 dp[i - 1][w - weight[i - 1][k]] + value[i - 1][k] 中最大值
                        dp[i][w] = max(dp[i][w], dp[i - 1][w - weight[i - 1][k]] + value[i - 1][k])

思路 1：复杂度分析

  • 时间复杂度：O(n×W×C)，其中 n 为物品分组数量，W 为背包的载重上限，C 是每组物品的数量。因为 n×C=∑groupcount[i]，所以时间复杂度也可以写成 O(W×∑groupcount[i])。
  • 空间复杂度：O(n×W)。

6.2 分组背包问题滚动数组优化

思路 2：动态规划 + 滚动数组优化

  1. 划分阶段

按照当前背包的载重上限进行阶段划分。

  1. 定义状态

定义状态 dp[w] 表示为：将物品装入最多能装重量为 w 的背包中，可以获得的最大价值。

  1. 状态转移方程

image-20240323120516778

  1. 初始条件
  • 无论背包载重上限为多少，只要不选择物品，可以获得的最大价值一定是 0，即 dp[w]=0,0≤w≤W。
  1. 最终结果

根据我们之前定义的状态， dp[w] 表示为：将物品装入最多能装重量为 w 的背包中，可以获得的最大价值。则最终结果为 dp[W]，其中 W 为背包的载重上限。

思路 2：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    # 思路 2：动态规划 + 滚动数组优化
    def groupPackMethod2(self, group_count: [int], weight: [[int]], value: [[int]], W: int):
        size = len(group_count)
        dp = [0 for _ in range(W + 1)]
        
        # 枚举前 i 组物品
        for i in range(1, size + 1):
            # 逆序枚举背包装载重量
            for w in range(W, -1, -1):
                # 枚举第 i - 1 组物品能取个数
                for k in range(group_count[i - 1]):
                    if w >= weight[i - 1][k]:
                        # dp[w] 取所有 dp[w - weight[i - 1][k]] + value[i - 1][k] 中最大值
                        dp[w] = max(dp[w], dp[w - weight[i - 1][k]] + value[i - 1][k])
                        
        return dp[W]

思路 2：复杂度分析

  • 时间复杂度：O(n×W×C)，其中 n 为物品分组数量，W 为背包的载重上限，C 是每组物品的数量。因为 n×C=∑groupcount[i]，所以时间复杂度也可以写成 O(W×∑groupcount[i])。
  • 空间复杂度：O(W)。

7. 二维费用背包问题

二维费用背包问题：有 n 件物品和有一个最多能装重量为 W、容量为 V 的背包。第 i 件物品的重量为 weight[i]，体积为 volume[i]，价值为 value[i]，每件物品有且只有 1 件。请问在总重量不超过背包载重上限、容量上限的情况下，能装入背包的最大价值是多少？

img

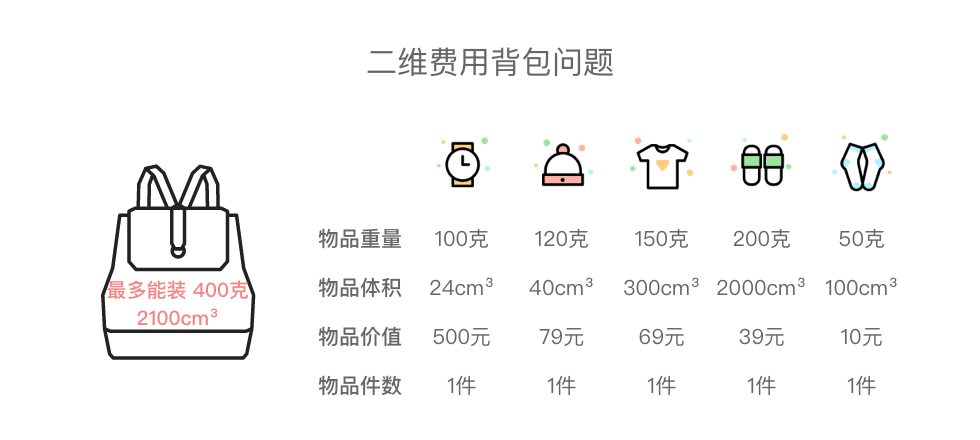
7.1 二维费用背包问题基本思路

我们可以参考「0-1 背包问题」的状态定义和基本思路，在「0-1 背包问题」基本思路的基础上，增加一个维度用于表示物品的容量。

思路 1：动态规划 + 三维基本思路

  1. 划分阶段

按照物品种类的序号、当前背包的载重上限、容量上限进行阶段划分

  1. 定义状态

定义状态 dp[i] [w] [v] 为：前 i 件物品放入一个最多能装重量为 w、容量为 v 的背包中，可以获得的最大价值。

  1. 状态转移方程

image-20240323120151351

  1. 初始条件
  • 如果背包载重上限为 0 或者容量上限为 0，则无论选取什么物品，可以获得的最大价值一定是 0，即：
    • dp[i] [w] [0]=0,0≤i≤size,0≤w≤W
    • dp[i] [0] [v]=0,0≤i≤size,0≤v≤V
  • 无论背包载重上限是多少，前 0 种物品所能获得的最大价值一定为 0，即：
    • dp[0] [w] [v]=0,0≤w≤W,0≤v≤V
  1. 最终结果

根据我们之前定义的状态， dp[i] [w] [v] 表示为：前 i 件物品放入一个最多能装重量为 w、容量为 v 的背包中，可以获得的最大价值。则最终结果为 dp[size] [W] [V]，其中 size 为物品的种类数，W 为背包的载重上限，V 为背包的容量上限。

思路 1：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    # 思路 1：动态规划 + 三维基本思路
    def twoDCostPackMethod1(self, weight: [int], volume: [int], value: [int], W: int, V: int):
        size = len(weight)
        dp = [[[0 for _ in range(V + 1)] for _ in range(W + 1)] for _ in range(size + 1)]
    
        # 枚举前 i 组物品
        for i in range(1, N + 1):
            # 枚举背包装载重量
            for w in range(W + 1):
                # 枚举背包装载容量
                for v in range(V + 1):
                    # 第 i - 1 件物品装不下
                    if w < weight[i - 1] or v < volume[i - 1]:
                        # dp[i][w][v] 取「前 i - 1 件物品装入装载重量为 w、装载容量为 v 的背包中的最大价值」
                        dp[i][w][v] = dp[i - 1][w][v]
                    else:
                        # dp[i][w][v] 取所有 dp[w - weight[i - 1]][v - volume[i - 1]] + value[i - 1] 中最大值
                        dp[i][w][v] = max(dp[i - 1][w][v], dp[i - 1][w - weight[i - 1]][v - volume[i - 1]] + value[i - 1])
                        
        return dp[size][W][V]

思路 1：复杂度分析

  • 时间复杂度：O(n×W×V)，其中 n 为物品分组数量，W 为背包的载重上限，V 为背包的容量上限。
  • 空间复杂度：O(n×W×V)。

7.2 二维费用背包问题滚动数组优化

思路 2：动态规划 + 滚动数组优化

  1. 划分阶段

按照当前背包的载重上限、容量上限进行阶段划分。

  1. 定义状态

定义状态 dp[w] [v]表示为：将物品装入最多能装重量为 w、容量为 v 的背包中，可以获得的最大价值。

  1. 状态转移方程

image-20240323115427547

  1. 初始条件
  • 如果背包载重上限为0或者容量上限为0，则无论选取什么物品，可以获得的最大价值一定是0，即：
    • dp[w] [0]=0,0≤w≤W
    • dp[0] [v]=0,0≤v≤V
  1. 最终结果

根据我们之前定义的状态， dp[w] [v] 表示为：将物品装入最多能装重量为 w、容量为 v 的背包中，可以获得的最大价值。则最终结果为 dp[W] [V]，其中 W 为背包的载重上限，V 为背包的容量上限。

思路 2：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:        
    # 思路 2：动态规划 + 滚动数组优化
    def twoDCostPackMethod2(self, weight: [int], volume: [int], value: [int], W: int, V: int):
        size = len(weight)
        dp = [[0 for _ in range(V + 1)] for _ in range(W + 1)]
        
        # 枚举前 i 组物品
        for i in range(1, N + 1):
            # 逆序枚举背包装载重量
            for w in range(W, weight[i - 1] - 1, -1):
                # 逆序枚举背包装载容量
                for v in range(V, volume[i - 1] - 1, -1):
                    # dp[w][v] 取所有 dp[w - weight[i - 1]][v - volume[i - 1]] + value[i - 1] 中最大值
                    dp[w][v] = max(dp[w][v], dp[w - weight[i - 1]][v - volume[i - 1]] + value[i - 1])
                    
        return dp[W][V]

思路 2：复杂度分析

  • 时间复杂度：O(n×W×V)，其中 n 为物品分组数量，W 为背包的载重上限，V 为背包的容量上限。
  • 空间复杂度：O(W×V)。

快来参与讨论吧~

博客近期分类标签归档
项目软件开发人工智能Staller
社交友链
更多关于本站
本站由 卡卡龙 使用 Stellar 1.29.1主题创建

本站访问量 次. 本文阅读量 次.

Stellar Copyright Licenses Hexo 备案 描述文字 描述文字