背包问题<三>

4. 多重背包问题

多重背包问题：有 n 种物品和一个最多能装重量为 W 的背包，第 i 种物品的重量为 weight[i]，价值为 value[i]，件数为 count[i]。请问在总重量不超过背包载重上限的情况下，能装入背包的最大价值是多少？

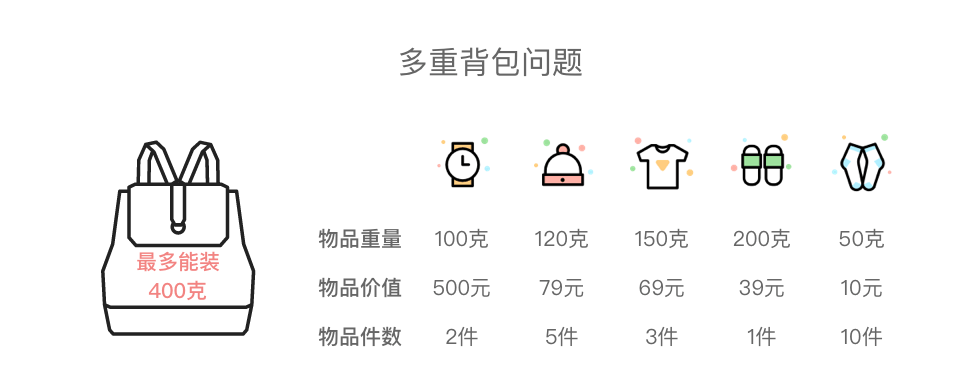
4.1 多重背包问题基本思路

我们可以参考「0-1 背包问题」的状态定义和基本思路，对于容量为 w 的背包，最多可以装

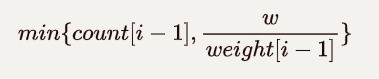
件第 i−1 件物品。那么我们可以多加一层循环，枚举第 i−1 件物品可以选择的件数

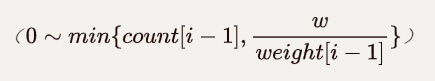
，从而将「完全背包问题」转换为「0-1 背包问题」。

思路 1：动态规划 + 二维基本思路

1. 划分阶段

按照物品种类的序号、当前背包的载重上限进行阶段划分。

2. 定义状态

定义状态 dp[i] [w] 表示为：前 i 种物品放入一个最多能装重量为 w 的背包中，可以获得的最大价值。

状态 dp[i] [w] 是一个二维数组，其中第一维代表「当前正在考虑的物品种类」，第二维表示「当前背包的载重上限」，二维数组值表示「可以获得的最大价值」。

3. 状态转移方程

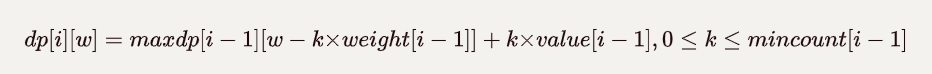
4. 初始条件

• 如果背包载重上限为 0，则无论选取什么物品，可以获得的最大价值一定是 0，即 dp[i] [0]=0,0≤i≤size。
• 无论背包载重上限是多少，前 0 种物品所能获得的最大价值一定为 0，即 dp[0] [w]=0,0≤w≤W。

5. 最终结果

根据我们之前定义的状态，dp[i] [w]表示为：前 i 种物品放入一个最多能装重量为 w 的背包中，可以获得的最大价值。则最终结果为 dp[size] [W]，其中 size 为物品的种类数，W 为背包的载重上限。

思路 1：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution:
    # 思路 1：动态规划 + 二维基本思路
    def multiplePackMethod1(self, weight: [int], value: [int], count: [int], W: int):
        size = len(weight)
        dp = [[0 for _ in range(W + 1)] for _ in range(size + 1)]
        
        # 枚举前 i 种物品
        for i in range(1, size + 1):
            # 枚举背包装载重量
            for w in range(W + 1):
                # 枚举第 i - 1 种物品能取个数
                for k in range(min(count[i - 1], w // weight[i - 1]) + 1):
                    # dp[i][w] 取所有 dp[i - 1][w - k * weight[i - 1] + k * value[i - 1] 中最大值
                    dp[i][w] = max(dp[i][w], dp[i - 1][w - k * weight[i - 1]] + k * value[i - 1])
                    
        return dp[size][W]

思路 1：复杂度分析

• 时间复杂度：O(n×W×C)，其中 n 为物品种类数量，W 为背包的载重上限，C 是物品的数量数组长度。因为 n×C=∑count[i]，所以时间复杂度也可以写成 O(W×∑count[i])。
• 空间复杂度：O(n×W)。

4.2 多重背包问题滚动数组优化

在「完全背包问题」中，我们通过优化「状态转移方程」的方式，成功去除了对物品件数 k 的依赖，从而将时间复杂度下降了一个维度。

而在「多重背包问题」中，我们在递推 dp[i] [w] 时，是无法从 dp[i] [w−weight[i−1]] 状态得知目前究竟已经使用了多个件第 i−1 种物品，也就无法判断第 i−1 种物品是否还有剩余数量可选。这就导致了我们无法通过优化「状态转移方程」的方式将「多重背包问题」的时间复杂度降低。

但是我们可以参考「完全背包问题」+「滚动数组优化」的方式，将算法的空间复杂度下降一个维度。

思路 2：动态规划 + 滚动数组优化

1. 划分阶段

按照当前背包的载重上限进行阶段划分。

2. 定义状态

定义状态 dp[w] 表示为：将物品装入最多能装重量为 w 的背包中，可以获得的最大价值。

3. 状态转移方程

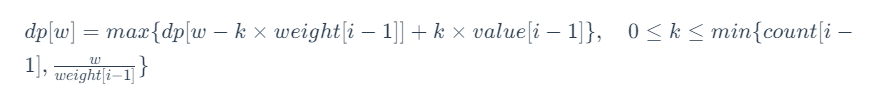
4. 初始条件

• 无论背包载重上限为多少，只要不选择物品，可以获得的最大价值一定是 0，即 dp[w]=0,0≤w≤W。

5. 最终结果

根据我们之前定义的状态， dp[w]表示为：将物品装入最多能装重量为 w 的背包中，可以获得的最大价值。则最终结果为 dp[W]，其中 W 为背包的载重上限。

思路 2：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

class Solution: 
    # 思路 2：动态规划 + 滚动数组优化
    def multiplePackMethod2(self, weight: [int], value: [int], count: [int], W: int):
        size = len(weight)
        dp = [0 for _ in range(W + 1)]
        
        # 枚举前 i 种物品
        for i in range(1, size + 1):
            # 逆序枚举背包装载重量（避免状态值错误）
            for w in range(W, weight[i - 1] - 1, -1):
                # 枚举第 i - 1 种物品能取个数
                for k in range(min(count[i - 1], w // weight[i - 1]) + 1):
                    # dp[w] 取所有 dp[w - k * weight[i - 1]] + k * value[i - 1] 中最大值
                    dp[w] = max(dp[w], dp[w - k * weight[i - 1]] + k * value[i - 1])
                
        return dp[W]

思路 2：复杂度分析

• 时间复杂度：O(n×W×C)，其中 n 为物品种类数量，W 为背包的载重上限，C 是物品的数量数组长度。因为 n×C=∑count[i]，所以时间复杂度也可以写成 O(W×∑count[i])。
• 空间复杂度：O(W)。

4.3 多重背包问题二进制优化

在「思路 2」中，我们通过「滚动数组优化」的方式，降低了算法的空间复杂度。同时也提到了无法通过优化「状态转移方程」的方式将「多重背包问题」的时间复杂度降低。

但我们还是可以从物品数量入手，通过「二进制优化」的方式，将算法的时间复杂度降低。

二进制优化：简单来说，就是把物品的数量 count[i]拆分成「由 1,2,4,…,2^m件单个物品组成的大物品」，以及「剩余不足 2 的整数次幂数量的物品，由 件单个物品组成大物品」。

举个例子，第 i 件物品的数量为 31，采用「二进制优化」的方式，可以拆分成 31=1+2+4+8+16 一共 5 件物品。也将是将 31 件物品分成了 5 件大物品：

1. 第 1 件大物品有 1 件第 i 种物品组成；
2. 第 2 件大物品有 2 件第 i 种物品组成；
3. 第 3 件大物品有 4 件第 i 种物品组成；
4. 第 4 件大物品有 8 件第 i 种物品组成；
5. 第 5 件大物品有 16 件第 i 种物品组成。

这 5 件大物品通过不同的组合，可表达出第 i 种物品的数量范围刚好是 0∼31。

这样本来第 i 件物品数量需要枚举共计 32 次（0∼31），而现在只需要枚举 5 次即可。

再举几个例子：

1. 第 i 件物品的数量为 6，可以拆分为 6=1+2+3 一共 3 件物品。
2. 第 i 件物品的数量为 8，可以拆分为 8=1+2+4+1 一共 4 件物品。
3. 第 i 件物品的数量为 18，可以拆分为 18=1+2+4+8+3 一共 5 件物品。

经过「二进制优化」之后，算法的时间复杂度从 O(W×∑count[i])降到了 O(W×∑log_⁡2count[i])。

思路 3：动态规划 + 二进制优化

1. 划分阶段

按照当前背包的载重上限进行阶段划分。

2. 定义状态

定义状态 dp[w] 表示为：将物品装入最多能装重量为 w 的背包中，可以获得的最大价值。

3. 状态转移方程
   

4. 初始条件

• 无论背包载重上限为多少，只要不选择物品，可以获得的最大价值一定是 0，即 dp[w]=0,0≤w≤W。

5. 最终结果

根据我们之前定义的状态， dp[w] 表示为：将物品装入最多能装重量为 w 的背包中，可以获得的最大价值。则最终结果为 dp[W]，其中 W 为背包的载重上限。

思路 3：代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution:
    # 思路 3：动态规划 + 二进制优化
    def multiplePackMethod3(self, weight: [int], value: [int], count: [int], W: int):
        weight_new, value_new = [], []
        
        # 二进制优化
        for i in range(len(weight)):
            cnt = count[i]
            k = 1
            while k <= cnt:
                cnt -= k
                weight_new.append(weight[i] * k)
                value_new.append(value[i] * k)
                k *= 2
            if cnt > 0:
                weight_new.append(weight[i] * cnt)
                value_new.append(value[i] * cnt)
        
        dp = [0 for _ in range(W + 1)]
        size = len(weight_new)
        
        # 枚举前 i 种物品
        for i in range(1, size + 1):
            # 逆序枚举背包装载重量（避免状态值错误）
            for w in range(W, weight_new[i - 1] - 1, -1):
                # dp[w] 取「前 i - 1 件物品装入载重为 w 的背包中的最大价值」与「前 i - 1 件物品装入载重为 w - weight_new[i - 1] 的背包中，再装入第 i - 1 物品所得的最大价值」两者中的最大值
                dp[w] = max(dp[w], dp[w - weight_new[i - 1]] + value_new[i - 1])
                    
        return dp[W]

思路 3：复杂度分析

• 时间复杂度：O(W×∑log⁡2count[i])，其中 W 为背包的载重上限，count[i] 是第 i 种物品的数量。
• 空间复杂度：O(W)。