算法：数组基础知识

1. 数组简介

1.1 数组定义

数组（Array）：一种线性表数据结构。它使用一组连续的内存空间，来存储一组具有相同类型的数据。

简单来说，「数组」 是实现线性表的顺序结构存储的基础。

以整数数组为例，数组的存储方式如下图所示。

数组存储方式 true

如上图所示，假设数据元素的个数为 n，则数组中的每一个数据元素都有自己的下标索引，下标索引从 0 开始，到 n − 1 结束。数组中的每一个「下标索引」，都有一个与之相对应的「数据元素」。

从上图还可以看出，数组在计算机中的表示，就是一片连续的存储单元。数组中的每一个数据元素都占有一定的存储单元，每个存储单元都有自己的内存地址，并且元素之间是紧密排列的。

我们还可以从两个方面来解释一下数组的定义。

线性表：线性表就是所有数据元素排成像一条线一样的结构，线性表上的数据元素都是相同类型，且每个数据元素最多只有前、后两个方向。数组就是一种线性表结构，此外，栈、队列、链表都是线性表结构。

连续的内存空间：线性表有两种存储结构：「顺序存储结构」和「链式存储结构」。其中，「顺序存储结构」是指占用的内存空间是连续的，相邻数据元素之间，物理内存上的存储位置也相邻。数组也是采用了顺序存储结构，并且存储的数据都是相同类型的。

综合这两个角度，数组就可以看做是：使用了「顺序存储结构」的「线性表」的一种实现方式。

1.2 如何随机访问数据元素

数组的一个最大特点是：可以进行随机访问。即数组可以根据下标，直接定位到某一个元素存放的位置。

那么，计算机是如何实现根据下标随机访问数组元素的？

计算机给一个数组分配了一组连续的存储空间，其中第一个元素开始的地址被称为 「首地址」。每个数据元素都有对应的下标索引和内存地址，计算机通过地址来访问数据元素。当计算机需要访问数组的某个元素时，会通过 「寻址公式」 计算出对应元素的内存地址，然后访问地址对应的数据元素。

寻址公式如下：下标 i 对应的数据元素地址 = 数据首地址 + i × 单个数据元素所占内存大小。

1.3 多维数组

上面介绍的数组只有一个维度，称为一维数组，其数据元素也是单下标变量。但是在实际问题中，很多信息是二维或者是多维的，一维数组已经满足不了我们的需求，所以就有了多维数组。

以二维数组为例，数组的形式如下图所示。

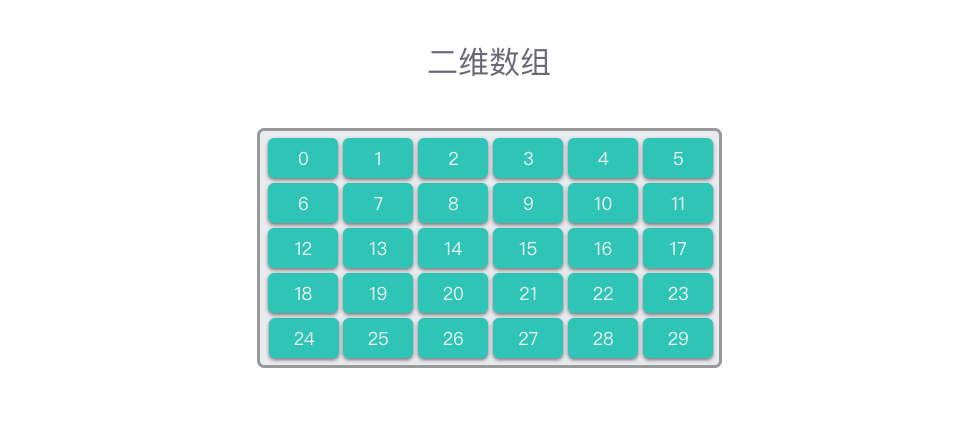
二维数组 true

二维数组是一个由 m 行 n 列数据元素构成的特殊结构，其本质上是以数组作为数据元素的数组，即 「数组的数组」。二维数组的第一维度表示行，第二维度表示列。

我们可以将二维数组看做是一个矩阵，并处理矩阵的相关问题，比如 转置矩阵、矩阵相加、矩阵相乘 等等。

1.4 不同编程语言中数组的实现

在具体的编程语言中，数组这个数据结构的实现方式具有一定差别。

C / C++ 语言中的数组最接近数组结构定义中的数组，使用的是一块存储相同类型数据的、连续的内存空间。不管是基本类型数据，还是结构体、对象，在数组中都是连续存储的。例如：

1	int arr[3][4] = {{0, 1, 2, 3}, {4, 5, 6, 7}, {8, 9, 10, 11}};

Java 中的数组跟数据结构定义中的数组不太一样。Java 中的数组也是存储相同类型数据的，但所使用的内存空间却不一定是连续（多维数组中）。且如果是多维数组，其嵌套数组的长度也可以不同。例如：

1	int[][] arr = new int[3][]{ {1,2,3}, {4,5}, {6,7,8,9}};

原生 Python 中其实没有数组的概念，而是使用了类似 Java 中的 ArrayList 容器类数据结构，叫做列表。通常我们把列表来作为 Python 中的数组使用。Python 中列表存储的数据类型可以不一致，数组长度也可以不一致。例如：

1	arr = ['python', 'java', ['asp', 'php'], 'c']

2. 数组的基本操作

数据结构的操作一般涉及到增、删、改、查共 4 种情况，下面我们一起来看一下数组的这 4 种基本操作。

2.1 访问元素

访问数组中第 i 个元素：

只需要检查 i 的范围是否在合法的范围区间，即 0 ≤ i ≤ len(nums)− 1。超出范围的访问为非法访问。

当位置合法时，由给定下标得到元素的值。

 // 从数组 nums 中读取下标为 i 的数据元素值
public void value(int[] nums, int i) {
    if (0 <= i && i <= nums.length - 1) {
            System.out.println(nums[i]);
    }
}

「访问数组元素」的操作不依赖于数组中元素个数，因此，「访问数组元素」的时间复杂度为 O(1)。

2.2 查找元素

查找数组中元素值为 val 的位置：

建立一个基于下标的循环，每次将 val 与当前数据元素 nums [i] 进行比较。

在找到元素的时候返回元素下标。

遍历完找不到时可以返回一个特殊值（例如 − 1）。

// 从数组 nums 中查找元素值为 val 的数据元素第一次出现的位置
public int find(int[] nums, int val) {
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] == val) {
            return i;
        }
    }
    return -1;
}

在「查找元素」的操作中，如果数组无序，那么我们只能通过将 val 与数组中的数据元素逐一对比的方式进行查找，也称为线性查找。而线性查找操作依赖于数组中元素个数，因此，「查找元素」的时间复杂度为 O(n)。

2.3 插入元素

插入元素操作分为两种：「在数组尾部插入值为 val 的元素」和「在数组第 i 个位置上插入值为 val 数组尾部插入值为 val 的元素：

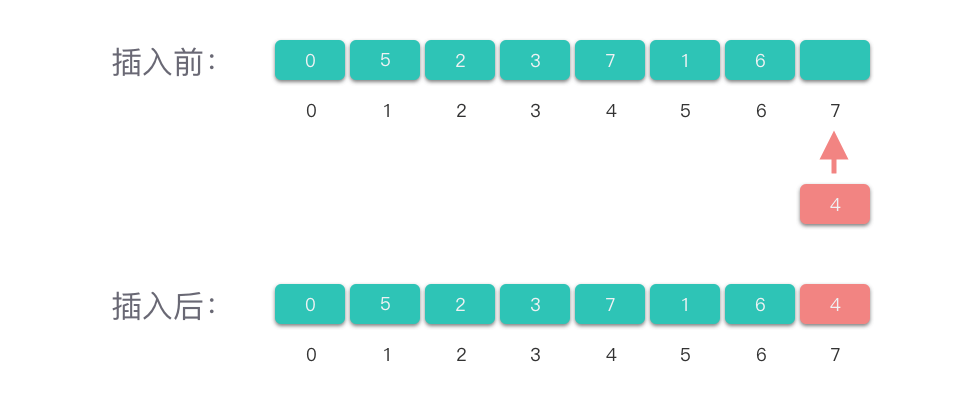
在数组尾部插入值为 val 的元素：

如果数组尾部容量不满，则直接把 val 放在数组尾部的空闲位置，并更新数组的元素计数值。

如果数组容量满了，则插入失败。不过，Python 中的 list 列表做了其他处理，当数组容量满了，则会开辟新的空间进行插入。

Python 中的 list 列表直接封装了尾部插入操作，直接调用 append 方法即可。

插入元素 true

List<Integer> arr = new ArrayList<>();
arr.add(0);
arr.add(5);
arr.add(2);
arr.add(3);
arr.add(7);
arr.add(1);
arr.add(6);
int val = 4;
arr.add(val);
System.out.println(arr);

「在数组尾部插入元素」的操作不依赖数组个数，因此，「在数组尾部插入元素」的时间复杂度为 O(1)。

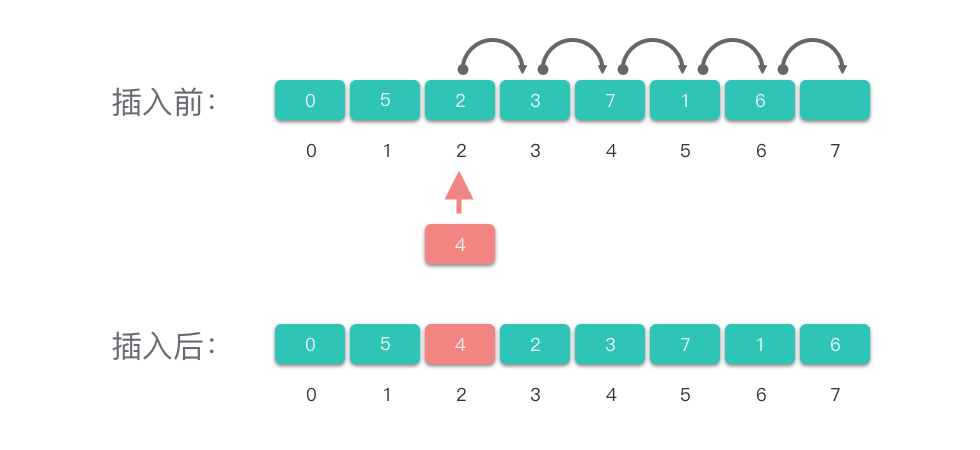
在数组第 i 个位置上插入值为 val 的元素：

先检查插入下标 i 是否合法，即 0 ≤ i ≤ len(nums)。

确定合法位置后，通常情况下第 i 个位置上已经有数据了（除非 i == len(nums)），要把第 i ∼ len(nums)− 1 位置上的元素依次向后移动。

然后再在第 i 个元素位置赋值为 v a l，并更新数组的元素计数值。

Python 中的 list 列表直接封装了中间插入操作，直接调用 insert 方法即可。

插入中间元素 true

List<Integer> arr = new ArrayList<>();
arr.add(0);
arr.add(5);
arr.add(2);
arr.add(3);
arr.add(7);
arr.add(1);
arr.add(6);
int i = 2;
int val = 4;
arr.add(i, val);
System.out.println(arr);

「在数组中间位置插入元素」的操作中，由于移动元素的操作次数跟元素个数有关，因此，「在数组中间位置插入元素」的最坏和平均时间复杂度都是 O(n)。

2.4 改变元素

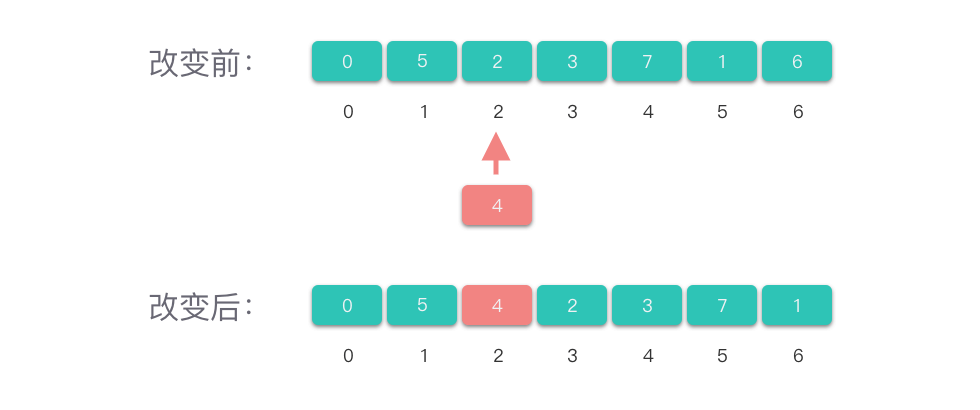
将数组中第 i 个元素值改为 val：

需要先检查 i 的范围是否在合法的范围区间，即 0 ≤ i ≤ len(nums)− 1。

然后将第 i 个元素值赋值为 val。

改变元素 true

// 修改数组 nums 中下标为 i 的元素值为 val
public static void change(int[] nums, int i, int val) {
    if (0 <= i && i <= nums.length - 1) {
        nums[i] = val;
    }
}

「改变元素」的操作跟访问元素操作类似，访问操作不依赖于数组中元素个数，因此，「改变元素」的时间复杂度为 O(1)。

2.5 删除元素

删除元素分为三种情况：「删除数组尾部元素」、「删除数组第 i 个位置上的元素」、「基于条件删除元素」。

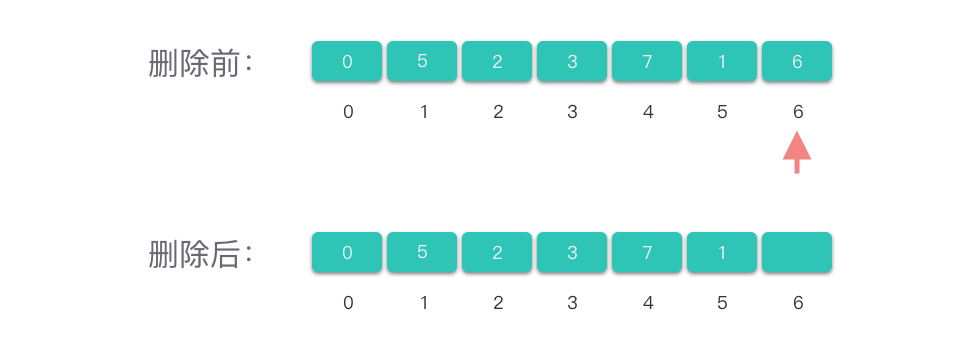
删除数组尾部元素：

只需将元素计数值减一即可。

Python 中的 list 列表直接封装了删除数组尾部元素的操作，只需要调用 pop 方法即可。

删除尾部元素 true

List<Integer> arr = new ArrayList<>();
arr.add(0);
arr.add(5);
arr.add(2);
arr.add(3);
arr.add(7);
arr.add(1);
arr.add(6);
arr.remove(arr.size() - 1);
System.out.println(arr);

「删除数组尾部元素」的操作，不依赖于数组中的元素个数，因此，「删除数组尾部元素」的时间复杂度为 O(1)。

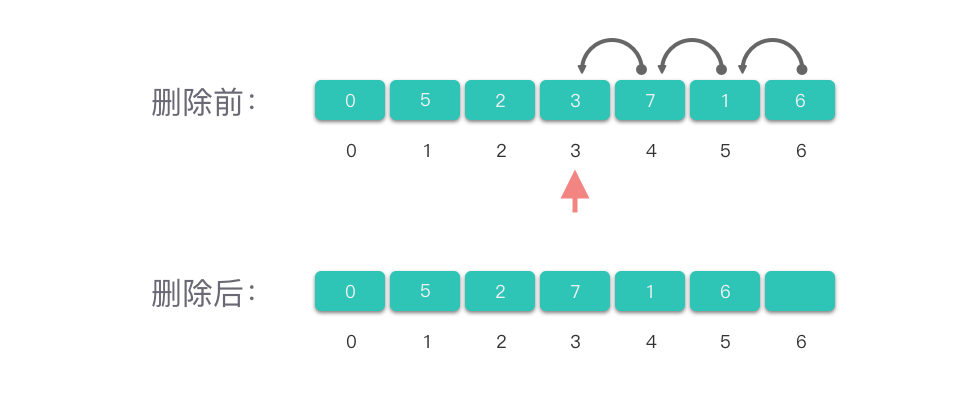
删除数组第 i 个位置上的元素：

先检查下标 i 是否合法，即 0 ≤ i ≤ len(nums)− 1。

如果下标合法，则将第 i+1 个位置到第 len(nums)− 1 位置上的元素依次向左移动。

删除后修改数组的元素计数值。

Python 中的 list 列表直接封装了删除数组中间元素的操作，只需要以下标作为参数调用 pop 方法即可。

删除中间元素

List<Integer> arr = new ArrayList<>();
arr.add(0);
arr.add(5);
arr.add(2);
arr.add(3);
arr.add(7);
arr.add(1);
arr.add(6);
int i = 3;
arr.remove(i);
System.out.println(arr);

「删除数组中间位置元素」的操作同样涉及移动元素，而移动元素的操作次数跟元素个数有关，因此，「删除数组中间位置元素」的最坏和平均时间复杂度都是 O(n)。

基于条件删除元素：这种操作一般不给定被删元素的位置，而是给出一个条件要求删除满足这个条件的（一个、多个或所有）元素。这类操作也是通过循环检查元素，查找到元素后将其删除。

List<Integer> arr = new ArrayList<>();
arr.add(0);
arr.add(5);
arr.add(2);
arr.add(3);
arr.add(7);
arr.add(1);
arr.add(6);
int val = 5;
arr.remove(Integer.valueOf(val));
System.out.println(arr);