1. 二叉树遍历简介

二叉树的遍历：指的是从根节点出发，按照某种次序依次访问二叉树中所有节点，使得每个节点被访问一次且仅被访问一次。

在二叉树的一些实际问题中，经常需要按照一定顺序对二叉树中每个节点逐个进行访问一次，用以查找具有某一特点的节点或者全部节点，然后对这些满足要求的节点进行处理。这里所说的「访问」就是指对该节点进行某种操作，例如：依次输出节点的数据信息、统计满足某条件的节点总数等等。

回顾二叉树的递归定义可以知道，二叉树是由根节点和左子树、右子树构成的。因此，如果能依次遍历这 3 个部分，就可以遍历整个二叉树。

如果利用深度优先搜索的方式，并且根据访问顺序次序的不同，我们可以分为 6 种遍历方式，而如果限制先左子树后右子树的遍历顺序，则总共有 3 种遍历方式：分别为 「二叉树的前序遍历」、「二叉树的中序遍历」 和 「二叉树的后续遍历」。

而如果使用广度优先搜索的方式，则可以按照层序方式（按照层次从上至下，每一层从左至右）对二叉树进行遍历，这种方式叫做 「二叉树的层序遍历」。

2. 二叉树的前序遍历

二叉树的前序遍历规则为：

  • 如果二叉树为空，则返回。
  • 如果二叉树不为空，则：
    1. 访问根节点。
    2. 以前序遍历的方式遍历根节点的左子树。
    3. 以前序遍历的方式遍历根节点的右子树。

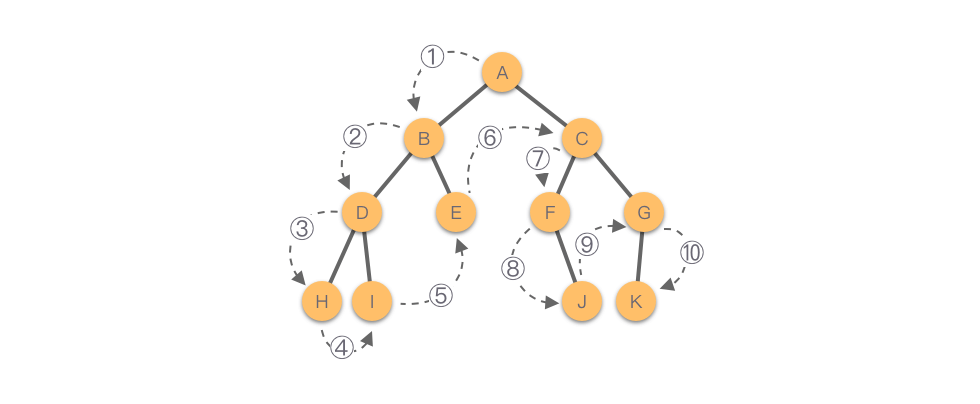
从二叉树的前序遍历规则可以看出：前序遍历过程是一个递归过程。在遍历任何一棵子树时仍然是按照先访问根节点，然后遍历子树根节点的左子树，最后再遍历子树根节点的右子树的顺序进行遍历。

如下图所示，该二叉树的前序遍历顺序为：𝐴−𝐵−𝐷−𝐻−𝐼−𝐸−𝐶−𝐹−𝐽−𝐺−𝐾。

二叉树的前序遍历

2.1 递归实现

二叉树的前序遍历递归实现步骤为：

  1. 判断二叉树是否为空，为空则直接返回。
  2. 先访问根节点。
  3. 然后递归遍历左子树。
  4. 最后递归遍历右子树。

二叉树的前序遍历递归实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}  
  
public class Solution {  
    public List<Integer> preorderTraversal(TreeNode root) {  
        List<Integer> res = new ArrayList<>();  
  
        preorder(root, res);  
        return res;  
    }  
  
    private void preorder(TreeNode root, List<Integer> res) {  
        if (root == null) {  
            return;  
        }  
        res.add(root.val);  
        preorder(root.left, res);  
        preorder(root.right, res);  
    }  
}

2.2 显示栈实现

二叉树的前序遍历递归实现的过程，实际上就是调用系统栈的过程。我们也可以使用一个显式栈 𝑠𝑡𝑎𝑐𝑘 来模拟递归的过程。

前序遍历的顺序为：根节点 - 左子树 - 右子树，而根据栈的「先入后出」特点，所以入栈的顺序应该为：先放入右子树，再放入左子树。这样可以保证最终遍历顺序为前序遍历顺序。

二叉树的前序遍历显式栈实现步骤如下：

  1. 判断二叉树是否为空，为空则直接返回。
  2. 初始化维护一个栈，将根节点入栈。
  3. 当栈不为空时：
    1. 弹出栈顶元素 𝑛𝑜𝑑𝑒，并访问该元素。
    2. 如果 𝑛𝑜𝑑𝑒的右子树不为空，则将 𝑛𝑜𝑑𝑒 的右子树入栈。
    3. 如果 𝑛𝑜𝑑𝑒 的左子树不为空，则将 𝑛𝑜𝑑𝑒 的左子树入栈。

二叉树的前序遍历显式栈实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}  
  
public class Solution {  
    public List<Integer> preorderTraversal(TreeNode root) {  
        List<Integer> res = new ArrayList<>();  
        if (root == null) {  
            return res; // 二叉树为空直接返回空列表  
        }  
  
        Stack<TreeNode> stack = new Stack<>();  
        stack.push(root);  
  
        while (!stack.isEmpty()) { // 栈不为空  
            TreeNode node = stack.pop(); // 弹出根节点  
            res.add(node.val); // 访问根节点  
  
            // 注意：前序遍历是先左后右，但栈是后入先出，所以要先将右子树入栈，再左子树入栈  
            if (node.right != null) {  
                stack.push(node.right); // 右子树入栈  
            }  
            if (node.left != null) {  
                stack.push(node.left); // 左子树入栈  
            }  
        }  
  
        return res;  
    }  
}

3. 二叉树的中序遍历

二叉树的中序遍历规则为：

  • 如果二叉树为空，则返回。
  • 如果二叉树不为空，则：
    1. 以中序遍历的方式遍历根节点的左子树。
    2. 访问根节点。
    3. 以中序遍历的方式遍历根节点的右子树。

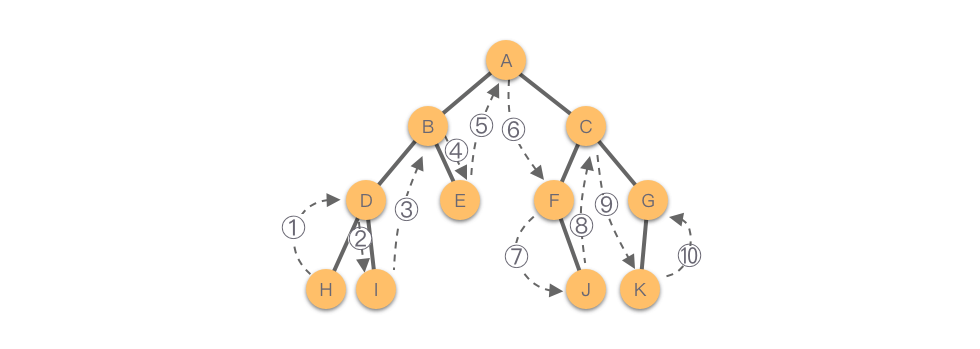
从二叉树的中序遍历规则可以看出：中序遍历过程也是一个递归过程。在遍历任何一棵子树时仍然是按照先遍历子树根节点的左子树，然后访问根节点，最后再遍历子树根节点的右子树的顺序进行遍历。

如下图所示，该二叉树的中序遍历顺序为：𝐻−𝐷−𝐼−𝐵−𝐸−𝐴−𝐹−𝐽−𝐶−𝐾−𝐺。

二叉树的中序遍历

3.1 递归实现

二叉树的中序遍历递归实现步骤为：

  1. 判断二叉树是否为空，为空则直接返回。
  2. 先递归遍历左子树。
  3. 然后访问根节点。
  4. 最后递归遍历右子树。

二叉树的中序遍历递归实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}  
  
public class Solution {  
    public List<Integer> inorderTraversal(TreeNode root) {  
        List<Integer> res = new ArrayList<>();  
        inorder(root, res);  
        return res;  
    }  
  
    private void inorder(TreeNode root, List<Integer> res) {  
        if (root == null) {  
            return;  
        }  
        inorder(root.left, res);  
        res.add(root.val);  
        inorder(root.right, res);  
    }  
}

3.2 显示栈实现

我们可以使用一个显式栈 𝑠𝑡𝑎𝑐𝑘来模拟二叉树的中序遍历递归的过程。

与前序遍历不同，访问根节点要放在左子树遍历完之后。因此我们需要保证：**在左子树访问之前，当前节点不能提前出栈**。

我们应该从根节点开始，循环遍历左子树，不断将当前子树的根节点放入栈中，直到当前节点无左子树时，从栈中弹出该节点并进行处理。

然后再访问该元素的右子树，并进行上述循环遍历左子树的操作。这样可以保证最终遍历顺序为中序遍历顺序。

二叉树的中序遍历显式栈实现步骤如下：

  1. 判断二叉树是否为空，为空则直接返回。
  2. 初始化维护一个空栈。
  3. 当根节点或者栈不为空时：
    1. 如果当前节点不为空，则循环遍历左子树，并不断将当前子树的根节点入栈。
    2. 如果当前节点为空，说明当前节点无左子树，则弹出栈顶元素 𝑛𝑜𝑑𝑒，并访问该元素，然后尝试访问该节点的右子树。

二叉树的中序遍历显式栈实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}  
  
public class Solution {  
    public List<Integer> inorderTraversal(TreeNode root) {  
        List<Integer> res = new ArrayList<>();  
        Stack<TreeNode> stack = new Stack<>();  
        TreeNode curr = root;  
  
        while (curr != null || !stack.isEmpty()) {  
            // 将当前节点的所有左子节点入栈  
            while (curr != null) {  
                stack.push(curr);  
                curr = curr.left;  
            }  
  
            // 栈顶元素出栈，并访问  
            TreeNode node = stack.pop();  
            res.add(node.val);  
  
            // 访问当前节点的右子树  
            curr = node.right;  
        }  
  
        return res;  
    }  
}

4. 二叉树的后序遍历

二叉树的后序遍历规则为：

  • 如果二叉树为空，则返回。
  • 如果二叉树不为空，则：
    1. 以后序遍历的方式遍历根节点的左子树。
    2. 以后序遍历的方式遍历根节点的右子树。
    3. 访问根节点。

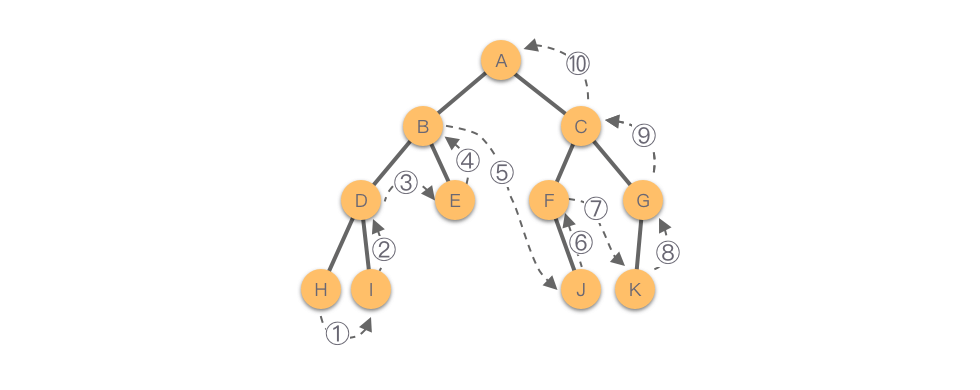
从二叉树的后序遍历规则可以看出：后序遍历过程也是一个递归过程。在遍历任何一棵子树时仍然是按照先遍历子树根节点的左子树，然后遍历子树根节点的右子树，最后再访问根节点的顺序进行遍历。

如下图所示，该二叉树的后序遍历顺序为：𝐻−𝐼−𝐷−𝐸−𝐵−𝐽−𝐹−𝐾−𝐺−𝐶−𝐴。

二叉树的后序遍历

4.1 递归实现

二叉树的后序遍历递归实现步骤为：

  1. 判断二叉树是否为空，为空则直接返回。
  2. 先递归遍历左子树。
  3. 然后递归遍历右子树。
  4. 最后访问根节点。

二叉树的后序遍历递归实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}  
  
public class Solution {  
    public List<Integer> postorderTraversal(TreeNode root) {  
        List<Integer> res = new ArrayList<>();  
        postorder(root, res);  
        return res;  
    }  
  
    private void postorder(TreeNode root, List<Integer> res) {  
        if (root == null) {  
            return;  
        }  
        postorder(root.left, res);  
        postorder(root.right, res);  
        res.add(root.val);  
    }  
}

4.2 显式栈实现

我们可以使用一个显式栈 𝑠𝑡𝑎𝑐𝑘 来模拟二叉树的后序遍历递归的过程。

与前序、中序遍历不同，在后序遍历中，根节点的访问要放在左右子树访问之后。因此，我们要保证：**在左右孩子节点访问结束之前，当前节点不能提前出栈**。

我们应该从根节点开始，先将根节点放入栈中，然后依次遍历左子树，不断将当前子树的根节点放入栈中，直到遍历到左子树最左侧的那个节点，从栈中弹出该元素，并判断该元素的右子树是否已经访问完毕，如果访问完毕，则访问该元素。如果未访问完毕，则访问该元素的右子树。

二叉树的后序遍历显式栈实现步骤如下：

  1. 判断二叉树是否为空，为空则直接返回。
  2. 初始化维护一个空栈，使用 𝑝𝑟𝑒𝑣 保存前一个访问的节点，用于确定当前节点的右子树是否访问完毕。
  3. 当根节点或者栈不为空时，从当前节点开始：
    1. 如果当前节点有左子树，则不断遍历左子树，并将当前根节点压入栈中。
    2. 如果当前节点无左子树，则弹出栈顶元素 𝑛𝑜𝑑𝑒。
    3. 如果栈顶元素 𝑛𝑜𝑑e 无右子树（即 not node.right）或者右子树已经访问完毕（即 node.right == prev），则访问该元素，然后记录前一节点，并将当前节点标记为空节点。
    4. 如果栈顶元素有右子树，则将栈顶元素重新压入栈中，继续访问栈顶元素的右子树。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}  
  
public class Solution {  
    public List<Integer> postorderTraversal(TreeNode root) {  
        List<Integer> res = new ArrayList<>();  
        Stack<TreeNode> stack = new Stack<>();  
        TreeNode prev = null; // 保存前一个访问的节点  
  
        while (root != null || !stack.isEmpty()) {  
            // 将当前节点的所有左子节点入栈  
            while (root != null) {  
                stack.push(root);  
                root = root.left;  
            }  
  
            TreeNode node = stack.pop();  
  
            // 如果当前节点没有右子树，或者右子树已经被访问过  
            if (node.right == null || node.right == prev) {  
                res.add(node.val); // 访问该节点  
                prev = node; // 记录前一节点  
                root = null; // 将当前根节点标记为空，继续外层循环判断  
            } else {  
                stack.push(node); // 右子树尚未访问完毕，将当前节点重新压回栈中  
                root = node.right; // 继续访问右子树  
            }  
        }  
  
        return res;  
    }  
}

5. 二叉树的层序遍历

二叉树的层序遍历规则为：

  • 如果二叉树为空，则返回。
  • 如果二叉树不为空，则：
    1. 先依次访问二叉树第 1 层的节点。
    2. 然后依次访问二叉树第 2 层的节点。
    3. ……
    4. 依次下去，最后依次访问二叉树最下面一层的节点。

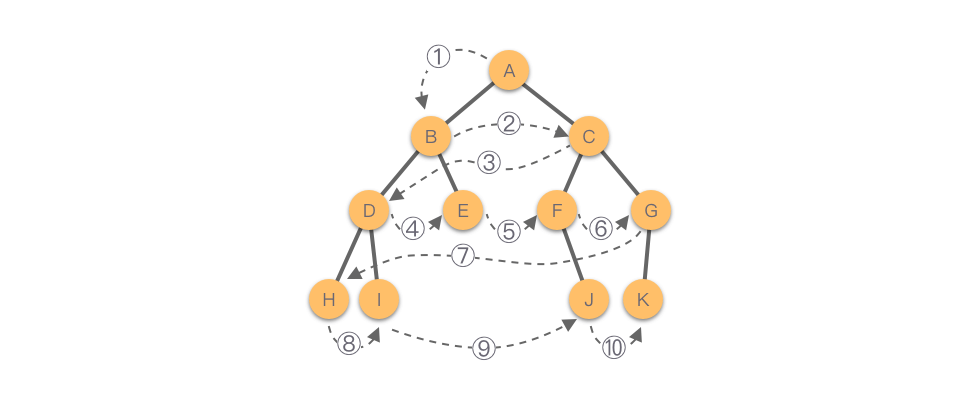
从二叉树的层序遍历规则可以看出：遍历过程是一个广度优先搜索过程。在遍历的时候是按照第 1 层、第 2 层、…… 最后一层依次遍历的，而同一层节点则是按照从左至右的顺序依次访问的。

如下图所示，该二叉树的后序遍历顺序为：𝐴−𝐵−𝐶−𝐷−𝐸−𝐹−𝐺−𝐻−𝐼−𝐽−𝐾。

二叉树的层序遍历二叉树的层序遍历

二叉树的层序遍历是**通过队列来实现**的。具体步骤如下：

  1. 判断二叉树是否为空，为空则直接返回。
  2. 令根节点入队。
  3. 当队列不为空时，求出当前队列长度 𝑠𝑖。
  4. 依次从队列中取出这 𝑠𝑖个元素，并对这 𝑠𝑖 个元素依次进行访问。然后将其左右孩子节点入队，然后继续遍历下一层节点。
  5. 当队列为空时，结束遍历。

二叉树的层序遍历代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class TreeNode {  
    int val;  
    TreeNode left;  
    TreeNode right;  
  
    TreeNode(int val) {  
        this.val = val;  
    }  
}  
  
public class Solution {  
    public List<List<Integer>> levelOrder(TreeNode root) {  
        List<List<Integer>> order = new ArrayList<>();  
        if (root == null) {  
            return order;  
        }  
          
        Queue<TreeNode> queue = new LinkedList<>();  
        queue.offer(root);  
          
        while (!queue.isEmpty()) {  
            List<Integer> level = new ArrayList<>();  
            int size = queue.size();  
              
            for (int i = 0; i < size; i++) {  
                TreeNode curr = queue.poll();  
                level.add(curr.val);  
                  
                if (curr.left != null) {  
                    queue.offer(curr.left);  
                }  
                  
                if (curr.right != null) {  
                    queue.offer(curr.right);  
                }  
            }  
              
            if (!level.isEmpty()) {  
                order.add(level);  
            }  
        }  
          
        return order;  
    }  
}

快来参与讨论吧~

博客近期分类标签归档
项目软件开发人工智能Staller
社交友链
更多关于本站
本站由 卡卡龙 使用 Stellar 1.29.1主题创建

本站访问量 次. 本文阅读量 次.

Stellar Copyright Licenses Hexo 备案 描述文字 描述文字